Case Report, J Nanomater Mol Nanotechnol Vol: 12 Issue: 2
Thermo Elastic Properties of Nanomaterials under High Compression
Anjani K Pandey*, Prachi Singh, Shivam Srivastava, Shipra Tripathi and Chandra K Dixit
Department of Physics, Shakuntala Misra National Rehabilitation University, Lucknow, India
*Corresponding Author: Anjani K Pandey
Department of Physics, Shakuntala Misra National Rehabilitation University, Lucknow, India; Tel: 8318482960; E-mail: anjani_phys@yahoo.in
Received date: 03 April, 2023, Manuscript No. JNMN-23-98279;
Editor assigned date: 07 April, 2023, PreQC No. JNMN-23-98279 (PQ);
Reviewed date: 21 April, 2023, QC No. JNMN-23-98279;
Revised date: 28 April, 2023, Manuscript No. JNMN-23-98279 (R);
Published date: 26 May, 2023, DOI: 10.4172/2324-8777.1000356
Citation: Pandey AK, Singh P, Srivastava S, Tripathi S, Dixit CK (2023) Thermo Elastic Properties of Nanomaterials under High Compression. J Nanomater Mol Nanotechnol 12:2.
Abstract
In this paper we have theoretically predicted some important thermo elastic properties of nanomaterials such as isothermal bulk modulus at different compressions, pressure derivative of isothermal bulk modulus and Gruneisen Parameter by using three different equation of states (I) Birch-Murnaghan (III) EOS, (II) Brennan-Stacey EOS and (III) Vinet-Rydberg EOS for 3C-SiC, Zr0.1Ti0.9O2, ε-Fe, Rb3C60 nanomaterials. The result shows that Gruneisen parameter decreases as compression increases. Also, the first pressure derivative of isothermal bulk modulus decreases as compression increases.
Keywords: Equation of States (EOSs), Nanomaterial, High-Pressure, Bulk Modulus, Gruneisen parameter
Introduction
High pressure research on nanomaterials are getting more attention between theoretical as well as experimental researchers, as at sufficiently high pressure a lot of structural effects happen inside nanomaterials viz. pressure ionization, change in electronic properties of nanomaterials etc. This can lead nanomaterials to change their physical, chemical and optical properties. Pressure is also connected with the Volume compression ratio (V/V0), bulk modulus (KT) and coefficient of volume expansion. Due to high thermal expansion, high chemical durability, strength and transparency of nanomaterials, it has also attracted attention in different commercial areas. The equation of state is a most useful tool to find the effect of pressure or compression over nanomaterials which leads to knowing the effect on thermoplastic properties such as volume compression, bulk modulus and effect of pressure on nanomaterials. The physical properties of nanomaterials depend on its structure and interatomic distances. if pressure is applied to the nanomaterials, due to pressure nanomaterial shows various effects, such as modification of interactions between the nano-object and pressure transmitting medium, transformations of non-constitutive elements and transformation of the interactions between the nanoobjects [1].
The gruneisen parameter (γ) is also directly related with EOSs at different pressure or compression. This theoretical approach is much useful for nanomaterials at different compressions for which no experimental data is available so for. Theoretical researchers have developed different EOSs for these purposes. In present work, we have used three different isothermal equation of states based on interatomic potential model viz. Birch- Murnaghan equation of state, Brennan-Stacey equation of state and Vinet-Rydberg equation of state to calculate the thermoelastic properties of 3C-SiC (Cubic Silicon- Carbide), Zr0.1Ti0.9O2 (Zr-doped nano anatase), ε-Fe (Epsilon iron) and Rb3C60 (Rubidium-doped C60) at high pressure [2].
Case Presentation
We have used three different equations of states, derived from lattice potential theory:
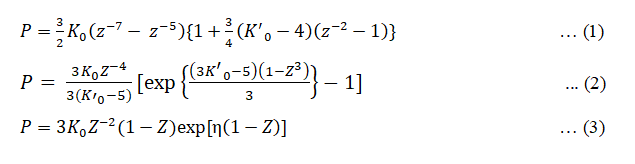
Where K0 and K0’ are isothermal bulk modulus and its first pressure derivative at zero pressure and
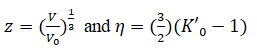
V is the volume at Pressure (P) and V0 is the volume at zero pressure. Equation (1) is based on Finite strain theory called Birch- Murnaghan (III order) EOS. Equation (2) based on thermodynamic Formulation for the Gruneisen parameter called Brennan-Stacey EOS. Equation (3) is the Vinet-Rydberg EOS and it is based on universal relationship between binding energy and interatomic separation for solids [3,4].
Form the equations (1), (2) and (3) we can obtain the expression for isothermal bulk modulus at Pressure (P):
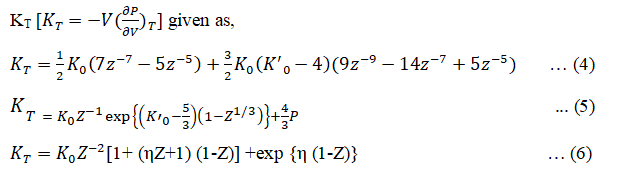
Using equations (4), (5) and (6) we can obtain the expression for K'T= (∂KT⁄∂P) the first derivative of isothermal bulk modulus at pressure P given as
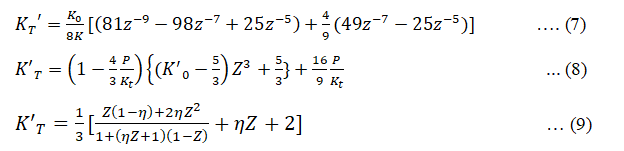
Thus equation (1), (4) and (7) represents the Birch-Murnaghan (III) EOS, equation (2), (5) and (8) represents Brennan-Stacey EOS and equation (3), (6) and (9) represents Vinet-Rydberg EOS respectively.
Grüneisen parameter (γ):
The expression for Gruneisen parameter as suggested by borton and Stacey given as,
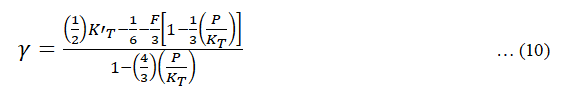
Where, F=2.35
Results and Discussion
In this work we have describe three different isothermal equation of states viz. Birch-Murnaghan equation of state, Brennan-Stacey equation of state and Vinet-Rydberg equation of state for calculating pressure, isothermal bulk modulus, first pressure derivative of isothermal bulk modulus and Grüneisen parameter at different compressions the value of Pressure (P) are calculated by using equation (1-3). The input value of K0 and K’0 are shown in Table 1. Further using the value are P in equation (4-6) We find value of KT further substituting the values are P and KT calculated by using equation (1-6) in equation (7-9) we find the values of K’T further substituting the values of P, KT and K’T obtain from equation (1-9) in equation (10) we obtain the value of Gruneisen parameter. The graphs are plotted between the calculated values of P at different compressions by using Birch-Murnaghan EOS, Brennan-Stacey EOS and Vinet-Rydberg EOS are shown in Figures 1-4. Further the graph plotted between V/V0 and KT are shown in Figures 5-8 the graph plotted between V/V0 and K’T are shown in Figures 9-12 and also the graph plotted between V/V0 and γ are shown in Figures. Equation (1), (4) and (7) represent the Birch-Murnaghan 3rd order EOS’s. Equation (2), (5) and (8) represent the Brennan-Stacy EOS’s and Equation (3), (6) and (9) represent the Vinet-Rydberg EOS’s and equation (10) represent the Gruneisen parameter respectively [5-8].
| Material | K0 (GPa) | K’0 |
|---|---|---|
| 3C-SiC | 245 | 2.9 |
| Zr0.1Ti0.9O2 | 213 | 17.9 |
| ε-Fe | 179 | 3.6 |
| Rb3C60 | 17.35 | 3.9 |
Table 1: Values of input data for K0 and K’0 is shown.
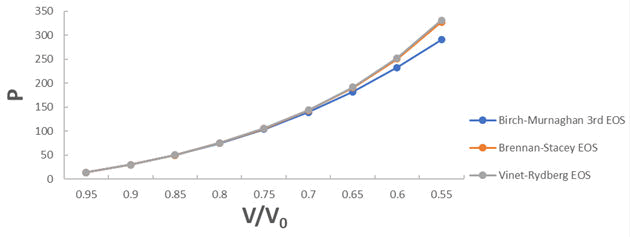
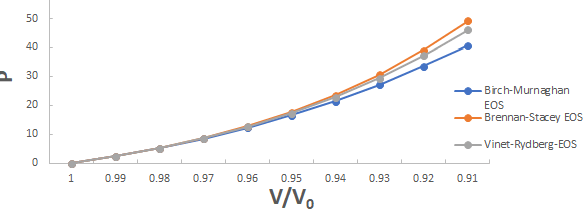
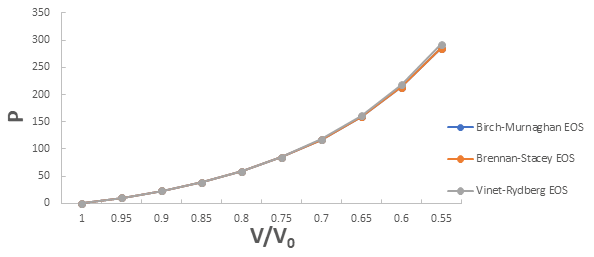
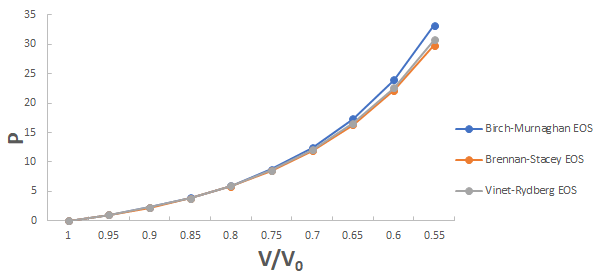
A graph plotted between P vrs V/V0 for 3C-SiC, Zr0.1Ti0.9O2, ε-Fe and Rb3C60 are shown in Figures 1-4.
From Figures 1-4 it is clear that on increasing the pressure, the value of compression increases for all the four nanomaterials viz. 3CSiC, Zr0.1Ti0.9O2, Rb3C60 and ε-Fe. Further for 3C-SiC all the three EOSs corresponds well upto volume compression range (V/V0)=0.7 at pressure 144 GPa then after the Brennan-Stacey EOS and Vinet- Rydberg EOS corresponds well with each other but the Birch- Murnaghan EOS starts deviating above the pressure 144 GPa with other two EOSs. Whereas for Zr0.1Ti0.9O2 and Rb3C60 all three EOSs corresponds well with each other upto compression range (V/V0)=0.95 at pressure 17.22 GPa and compression range (V/V0)=0.7 at Pressure 12.05 GPa respectively then after all the three EOSs starts deviating with each other. For ε-Fe the Brennan-Stacey EOS, Vinet-Rydberg EOS and Birch-Murnaghan EOS corresponds well with each other over entire compression range [9-11].
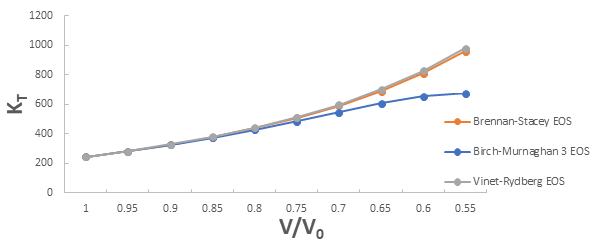
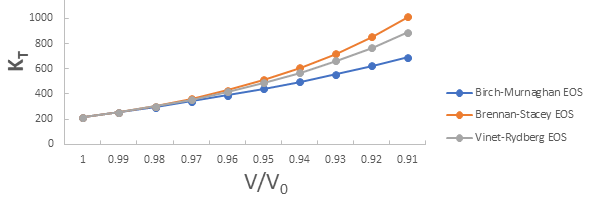
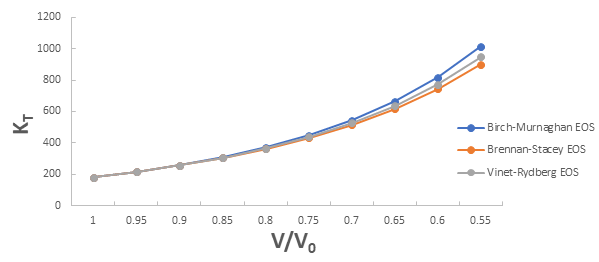
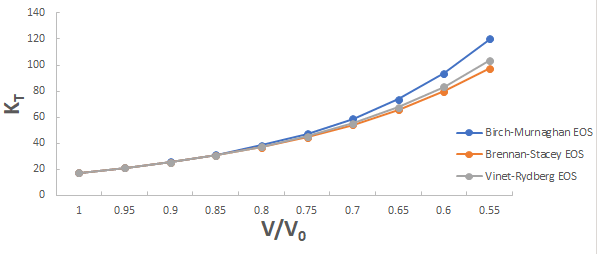
Further the graph for isothermal bulk modulus versus compression for 3C-SiC, Zr0.1Ti0.9O2, ε-Fe and Rb3C60 are shown in Figures 5-8.
From Figure 5-8 it is clear that on increasing the pressure, the value of compression increases for all the four nanomaterials viz. 3C-SiC, Zr0.1Ti0.9O2, Rb3C60 and ε-Fe. Further for 3C-SiC all three EOSs corresponds well upto compression range (V/V0) 0.8 at isothermal bulk modulus 440 GPa but after that the Birch-Murnaghan EOS starts deviate with other two EOSs. Whereas for Zr0.1Ti0.9O2, ε-Fe and Rb3C60 all three EOSs corresponds well upto compression range (V/ V0)=0.97 at isothermal bulk modulus 354.82 GPa, compression range (V/V0)=0.75 at isothermal bulk modulus 438.44 GPa and compression range (V/V0)=0.85 at isothermal bulk modulus 30.88 GPa respectively but all the Brennan-Stacey EOS, Vinet-Rydberg EOS and Birch- Murnaghan EOS starts deviating above the isothermal bulk modulus 354.82 GPa, 438.44 and 30.88 with each other [12-15].
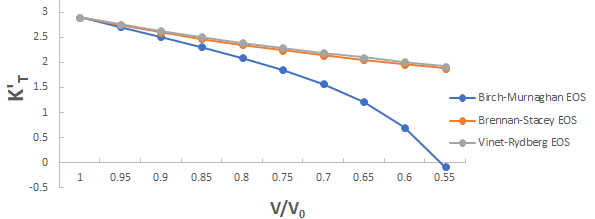
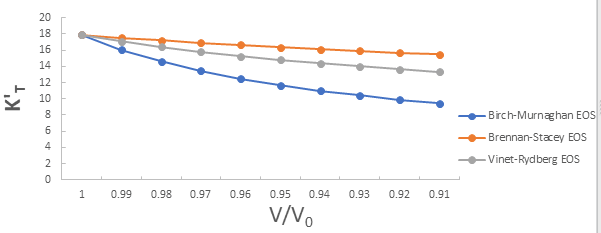
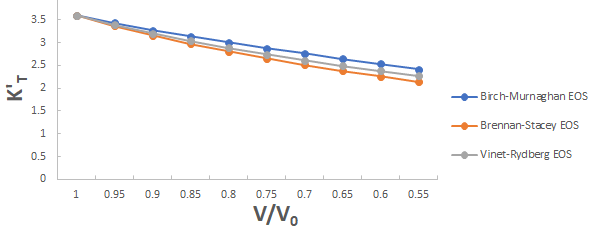
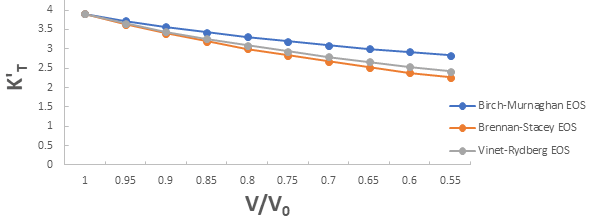
Further the graph for first pressure derivative of isothermal bulk modulus versus compression for 3C-SiC, Zr0.1Ti0.9O2, ε-Fe and Rb3C60 are shown in Figures 9-12.
From Figures 9-12 it is clear that on decreasing first pressure derivative of isothermal bulk modulus, the value of compression increases for all the four nanomaterials 3C-SiC, Zr0.1Ti0.9O2, Rb3C60 and ε-Fe. Further for 3C-SiC the Brennan-Stacey EOS and Vinet- Rydberg EOS corresponds well with each other but the Birch- Murnaghan EOS starts deviating below compression range V/V0=0.95 at first pressure derivative of isothermal bulk modulus 2.7 with other two EOSs. Whereas for Zr0.1Ti0.9O2, ε-Fe and Rb3C60 all the three EOSs (Brennan-Stacey EOS and Vinet-Rydberg EOS and Birch- Murnaghan EOS) does not Corresponds with each other entire compression range. Further the graph for Gruneisen parameter (γ) versus compression for 3C-SiC, Zr0.1Ti0.9O2, ε-Fe and Rb3C60 are shown [16].
Conclusion
It is clear that on decreasing Grüneisen parameter, the value of compression increases for all the four nanomaterials 3C-SiC, Zr0.1Ti0.9O2, Rb3C60 and ε-Fe. Further for 3C-SiC all three EOSs corresponds well upto compression range=0.9 at Grüneisen parameter 0.45 then after the Brennan-Stacey EOS and Vinet-Rydberg EOS are corresponds well with each other but Birch-Murnaghan EOS start deviating below upto Grüneisen parameter 0.45 with each other two EOSs. Whereas for Zr0.1Ti0.9O2, ε-Fe and Rb3C60 all the three EOSs does Corresponds with each other entire compression range.
References
- San-Miguel A (2006) Nanomaterials under high-pressure. Chem Soc Rev 35: 876-889.
- Chaurasiya R, Auluck S, Dixit A (2018) Cation modified A2 (Ba, Sr and Ca) ZnWO6 cubic double perovskites: A theoretical study. Com Cond Mat 14: 27-35.
- Zhou O, Zhu QING, Fischer JE, Coustel N, Vaughan GB, et al. (1992) Compressibility of M3C60 fullerene superconductors: Relation between Tc and lattice parameter. Science 255: 833-835.
- Chen B, Penwell D, Kruger MB, Yue AF, Fultz B, et al. (2001) Nanocrystalline iron at high pressure. J App Phy 89: 4794-4796.
- Liu H, Jin C, Chen J, Hu J (2004) anomalous dynamical charge change behavior of nanocrystalline 3c‐sic upon compression. J Amer Ceram Soc 87: 2291-2293.
- Kuo MH (2011) Opportunities and challenges of cloud computing to improve health care services. J Med Intern Res 13: e1867.
[Crossref] [Google Scholar] [PubMed]
- Lizy RF (2021) Improvement of RSA algorithm using euclidean technique. Turk J Comp Math Educ 12: 4694-4700.
- Shankar M, Akshaya P (2014) Hybrid cryptographic technique using RSA algorithm and scheduling concepts. Intern J Netw Sec App 6: 39.
- Sun P (2020) Security and privacy protection in cloud computing: Discussions and challenges. J Network Comp App 160: 102642.
- Ouahmane H, Kartit A, Marwan M (2018) A secured data processing technique for effective utilization of cloud computing. J Data Min Digital Humanities.
- Ukwuoma HC, Arome G, Thompson A, Alese BK (2022) Post-quantum cryptography-driven security framework for cloud computing. Open Comp Sci 12: 142-153.
- Zeng P, Chen S, Choo KK (2019) An IND-CCA2 secure post-quantum encryption scheme and a secure cloud storage use case. Human-Centric Comput Inform Sci 9: 1-5.
- El Balmany C, Tbatou Z, Asimi A, Bamarouf M (2022) Secure virtual machine image storage process into a trusted zone-based cloud storage. Comp Sec 120: 102815.
- Liu Z, Choo KK, Grossschadl J (2018) Securing edge devices in the post-quantum internet of things using lattice-based cryptography. IEEE Communications Magazine 56: 158-162.
- Balogh S, Gallo O, Ploszek R, Spacek P, Zajac P (2021) IoT security challenges: Cloud and blockchain, postquantum cryptography and evolutionary techniques. Electronics 10: 2647.
- Kumar A, Ottaviani C, Gill SS, Buyya R (2022) Securing the future internet of things with post‐quantum cryptography. Sec Privacy 5: e200.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi