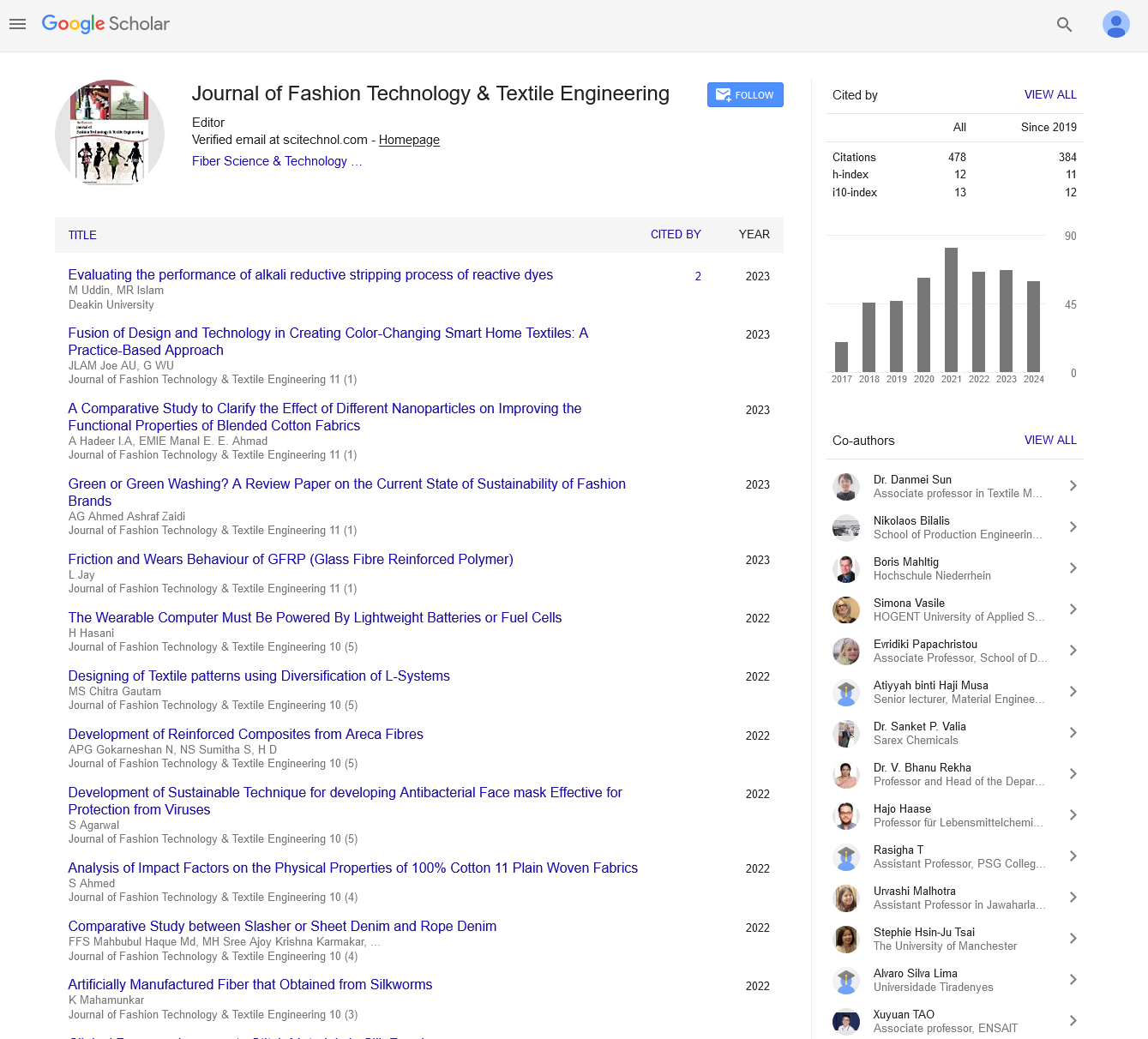
Research Article, J Fashion Technol Textile Eng Vol: 6 Issue: 2
Measurement of the Coefficient of Absorption and Reflection in Textile Materials with the Model Spctral2
Ruiz-Hernandez O, Tolentino-Eslava P, Robledo-Sanchez C and Montes-Perez A*
Facultad de Ciencias Físico Matemáticas, Benemérita Universidad Autónoma de Puebla, México
*Corresponding Author : Montes Pérez Areli
Research Professor, Facultad de Ciencias Físico Matemáticas, Benemérita Universidad Autónoma de Puebla, Avenida San Claudio y 18 Sur
Colonia San Manuel, Edificio FM1-101B, Ciudad Universitaria, C.P, 72570, Puebla, México
Tel: +52(222)2295500 (extn 3674)
E-mail: arelimp@fcfm.buap.mx
Received: June 06, 2018 Accepted: June 27, 2018 Published: July 02, 2018
Citation: Ruiz-Hernandez O, Tolentino-Eslava P, Robledo-Sanchez C, Montes-Perez A (2018) Measurement of the Coefficient of Absorption and Reflection in Textile Materials with the Model Spctral2. J Fashion Technol Textile Eng 6:2. doi:10.4172/2329-9568.1000173
Abstract
The chemical staining treatment on a textile material, define the color of each one. The dark color with a very low reflectance value, tend to reflect less light and absorb more thermal energy, on the other hand the light color with high reflectance value absorb less thermal energy. In this paper, with the SPCTRAL2 model describes that the solar irradiance flux that reaches the terrestrial surface, we calculate the absorption and reflection coefficients of certain textile materials of different colors.
Keywords: Absorption coefficients; Refection coefficients; SPCTRAL2 model; Textile materials
Introduction
In recent years to global level, the orientation of the researches on renewable energy was considerably increased with a great world impact. The solar energy is the most promising renewable energy, as is considered like an inexhaustible energy source. The solar energy that reaches the earth´s surface is vitally important on several research field includes climatic studies, atmospheric physics, photovoltaic application and solar thermal applications [1]. On the other hand, from the strict physics point of view, when the solar radiation fall upon a textile material, some of the next situations will have place, the solar radiation will be scattered, absorbed or reflected, the situations before mentioned depend of the color and texture from the textile.
Nowadays, is good known that the amount of light reflected is called value of luminous reflectance from color [2]. The dark colors with low level of luminous reflectance tend to reflect less light and absorbs great thermal energy, meanwhile the light colors with biggest luminous reflectance level reflects great amount of light and absorbs little thermal energy, this is strongly connected with the chemical treatment of textile staining, since the textile material is treated with Titanium oxide, Zinc oxide, Aluminum or Silicate or some other materials, due to the high reflectance level prevents that the tissues get heated and like a consequence, absorb less energy. In the literature is reported experimental researches about absorbent materials of solar energy for the hot water supply [3], other authors report studies through interferometric techniques determine the refractive index on fibers, likewise acoustic methods are employed for the measurement of the density and the mechanical losing factor on fibers, all of this for explain thermal effects on same [4]. On the other hand, the authors Pomfret et al. report studies about Young module and the electric conductivity on fibers [5].
On this article, diverse textile materials are studied for experimentally measuring the thermal irradiance emitted for every material, all this after the materials were exposed to the sun for a lapse time. The thermal irradiance analysis and the spectral irradiance model SPCTRAL2 allow us to find the absorption and reflection coefficients of every material, under consideration that the materials acts like opaque bodies.
Considerations Related with Solar Radiation
The radiation can be defined like the energy transference without a ponderable intermediate media, the thermal radiation is emitted due to the temperature of a body, however to difference of other kinds of heat transference, this does not flow from a body with high temperature to another with lower temperature, it means that if there are two bodies emitting radiation, exist a net flux of radiation between the bodies. The intensity of the radiation, is the amount of light and heat received on a surface bathed for the sun rays in a determined time unit, it is called solar irradiance and this depends on first place of the incident angle of the rays [6]. The Sun is a completely gaseous star, which has a temperature on his surface around 5777º Kelvin, and his nucleus is 15 millions of degrees Kelvin approximately, in which has place nuclear fusion reactions between Hydrogen atoms and that result in Helium atoms, that process release radiation that is scattered with the same intensity in all directions, this is named solar radiation, and it can pass through the interplanetary media and arrive to the Earth from the Sun. Now, from the black body radiation theory described for Planck, we can consider that the Sun is like a black body to 5777º Kelvin, distributing the 98% of the received energy in a surface between wavelengths from 0.25 to 3 micrometers.
In order to find all the amount of thermal radiation emitted from a body, is necessary to consider the contribution of all the wavelengths, if we integrate the spectral distribution of Planck respect to the wavelength, we can find the Stefan-Boltzmann law, which depends on the body temperature which emits radiation [7]. Using the Stefan-Boltzmann law, we can mathematically express the total energy emitted from the Sun that arrives to the Earth, considering that the energy does not vary his course from the Sun to the Earth surface.
We define the solar constant like the solar radiation that incides on the Earth surface by square meter, this is, the solar irradiance when the Sun is a middle distance Earth-Sun, such distance varies 1.7% per year [8].
The earth orbits around the Sun is an elliptical movement (Figure 1), as a result there is a day of the year in which the Earth is more close to the Sun (January 3) and another day in which is more distant (July 4), however, there are two points in which the Earth is at the same distance from the Sun (April 4 and October 5), due to the translation movement of the Earth around the Sun, which causes that the radiant energy depends of the day of the year. If we consider the rotational movement towards the Earth, it is necessary to introduce the concept of Earth’s declination, which is the angle between the straight line that connect the Earth’s centers and the Sun respect to the terrestrial equatorial plane, this angle oscillates between 23º27’ and -23º27’, taking the positive value between June 21 and 22, and the negative value between December 21 and 22, dates known as summer and winter entrance respectively. On the other hand, takes a null value between March 20 and 21, and between September 22 and 23, spring and autumn entrances respectively.
Now, in order to consider the incident irradiance on a surface which is inside the Earth, is necessary to know the incident angle with which the Sun rays reaches that surface (Figure 2), this drives us to define a reference system where the position of the Sun and the surface can be referred to, if we do not take on account the variation between the Earth-Sun distance, such movements can be represented on the celestial sphere, where suppose an equivalent fictitious movement in which every astro turns around the Earth, (Figure 3). In the celestial sphere, is supposed to the Earth with the vertical axis and the north pole pointing up, with that supposition the sun will realize a movement over horizontal circumferences with a height that depends of the declination, also in 24 h, the angle must make a completely circumference, this means that has an approximate velocity of 15º/h, another consideration is that the origin is established through the null hour angle in the moment in that the sun is at the highest point over the horizon. So the radiation emitted by the sun will change when this enters to the Earth’s surface like the solar incident irradiance out of the atmosphere by the cosine of the incident angle of the sun rays.
It is well known that the atmosphere is composed of different gaseous molecules and particles of different sizes, all of this produce the absorption, reflection or scattering of the radiation in certain wavelengths, for this reason the solar radiation that pass through the atmosphere is reduced and is not only emitted on the sun rays direction (Figure 4). Such scattering is considered isotropic, this produces direct (In) and diffuse (Id) radiation. The interaction of the solar radiation with the different compounds of the atmosphere is quite complicated of describe analytically, however, exists several numerical models that were developed with the pass of the years. On this work was employed the spectral irradiance model SPCTRAL2 for finding the total solar irradiance on a surface inside the terrestrial atmosphere, this election was made because SPCTRAL2 is one of the models that is better adjusted to the experimental data.
SPCTRAL2 Model
Literature reports that to finding the solar radiation that passes through the atmosphere and reaches a horizontal surface to certain height over the sea level, it is used the spectral irradiance model SPCTRAL2, which was proposed by Bird and Riordan [9], based on the previous works of Leckner [10], as well as the works of Nann and Riordan [11], Brine and Iqbal [12], who introduced some corrections and modifications for improve the predictions of the model, basing on the comparison of the validity of the model with measured spectra and radiative transference results. The SPCTRAL2 model is based on the products of empirical transmission functions for the most important processes of atmospheric extinction, such that, air molecules, ozone, water steam, gases mixtures and aerosol sprays. The product of the transmission functions for predict the transmitted beam irradiance modify the spectral radiation of the direct beam. Using the extraterrestrial solar spectra of Neckel and Labs [13], the SPCTRAL2 code calculates the direct beam and the diffuse components employing like entry parameters local geographic coordinates, atmospheric pressure, precipitated water and aerosol optical depth. We used the SPCTRAL2 model for finding the received solar irradiance for every material and this way calculates the desired absorption and reflection coefficients.
Procedure and Experimental Results
The experimental implementation to measure the thermal radiation in the textile materials, was driven on a clear day between 12:00 and 14:30 h. The textile materials used are, Polar smooth, Lycra, Tergal, Paladin, Liverpool gabardine, Poplin and Denim, being a total of 22 samples of these in different colors, each of one with 625 cm2, the Table 1 shows the composition of every material.
| Material | Composition |
|---|---|
| Polar smooth | 100% polyester |
| Lycra | 90% cotton, 10% spandex |
| Terga | 100% polyester |
| Paladin | 100% polyester |
| Liverpool gabardine | 100% cotton |
| Poplin | 65% cotton, 35% polyester |
| Denim | 100% cotton |
Table 1: Textile materials used for experimental measurements and their composition.
The samples are placed on a flat surface and exposed to the Sun for 10 min, after that, measurements of every textile material are taken with a thermal radiation sensor (thermopile) PASCO brand, model TD-8553, which has a spectral response from 0.5 μm to 40 μm and an approximate sensibility of 22 mV/mW, the sensor is connected to a multimeter, for monitory the thermal radiation emitted for each textile material on millivolts, the sensor was placed ortonormal to the textile material and every measurement was taken at a 10 min gap (Figure 5).
The measurements of each textile material sample, were registered and later were plotted the thermal irradiance emitted vs. the date time, the measurements have made from the year 2015 to 2017 in different dates, this with the objective of have a better reference about the present work. Each of one of the graphs show the emitted irradiance comportment for every textile material on their different colors, as well as the registration dates when they were taken (Figures 6-8). The obtained information like year date, hour and geographic zone were used on the SPCTRAL2 model, and this way to calculate the solar irradiance that passed through the terrestrial surface in that dates.
According the black body radiation theory, we would expect that the black color materials should emit more radiation than the others, however, from the graphs we look that this does not happen in all the cases, on the other hand we can see that the radiation emission is different for the different colors, something expected, since the studies about luminous reflectance of the color, indicate us that the color of the material is related to the reflectance. The white color, in every cases, emits the lower radiation, this result coincides with the theoretical prediction.
Absorption and reflection coefficients
From the graphs, we seek an interval of time where the measurements of emitted radiation for every textile material, is approximately the same value, this means that the curve has an approximately constant comportment on a time interval, we suppose that on those intervals of time the material have reached an approximate thermal equilibrium state, from the Stefan-Boltzmann law we deduce that if the emitted radiant energy is approximately constant then their temperature are constant too. From the Kirchhoff gray bodies law, we can establish that the absorption coefficient is the same as the emission coefficient, furthermore the process occur in some micrometers deep and each textile material has an approximate width of 1 mm, we can suppose that the materials are opaque’s bodies, and hence we can know the absorption and reflection coefficients.
To obtain the absorption and reflection coefficients, the measured values of emitted radiation that are considered constants, were averaged and after that the solar irradiance emitted is quantified, which was obtained using the SPCTRAL2 model, that model was obtained from [14]. In Figure 9, we appreciate that the curves of solar irradiance obtained from the SPCTRAL2 model in the indicated date of the year.
Figure 9: Solar radiation obtained by the SPCTRAL2 , a) November 06 2015, where Polar Smooth and Lycra: all colors, Poplin: sky blue, lime, Denim: blue, black, they have been graphed. b) October 15 2016, where Polar Smooth and Lycra: all colors, Gabardine: red, blue, lime, Tergal: brown, beige, Paladin: grey, dark green, Poplin: sky blue, Denim: black, blue, they have been graphed. c) May 2017, where Polar Smooth and Lycra: all colors, Gabardine: red, lime, blue, Tergal: brown, beige, Paladin: grey, lime, Poplin: sky blue, Denim: black, blue, they have been graphed.
On these curves, we observe spectra of direct solar irradiance, diffuse, total, global std and direct std (Standard Solar Spectral). The Direct, Diffuse and Total spectra, corresponds to the direct, diffuse and total irradiance received respectively, over a body placed parallel to the earth´s surface, this means a body without inclination respect the earth´s surface; the Global std and Direct std spectra correspond to the global standard specter and the direct standard solar radiation, whose are obtained from solar radiation experimental data, these are inside the SPCTRAL2 model. We can see from the Global std and Total spectra that these overlap well for the 2016 dates, however this does not happened for the 2015, furthermore is considerably to mention that the maximum irradiance obtained from the model was from the 2016; for the 2017 the total irradiance obtained from the model is more than the global std. We can attribute this can behavior to that the SPCTRAL2 model is for clear skies and the formation of some clouds that cannot be prevent, can change the solar irradiance monitored, this can be reflected on the parameters like the water precipitation, which can generate some variations between the solar standard spectra and the calculated spectra.
Now is possible calculate the radiation emission coefficient of each textile material, with aid of the radiation amount received and emitted, mathematically expressed like
εISun = Imaterial (1)
Where �? is the emission coefficient of the material. After obtain the emission coefficient, we were able to find the absorption and reflection coefficients, and later we compare these coefficients for determine the more absorbent material and the more reflective. The results obtained are showed in the Table 2.
Results and Discussions
The emitted radiation measured of each textile material on different dates and years versus the hour, allows considering a constant comportment in some interval of time, where we suppose that the material reaches its thermal equilibrium, this from the Stefan- Boltzmann Law. From Kirchhoff gray bodies law, we suppose that the analyzed materials act as opaque bodies and hence we can know his absorption and reflection coefficient of each material. The hour, date and year of each measure realized, are used on the SPCTRAL2 model, for quantify the irradiance emitted from the Sun on those dates. The solar irradiance curves obtained from the SPCTRAL2 model are irradiance curves received of the next ways direct, diffuse or total, over a body with an orientation parallel to the earth´s surface. The denoted spectra like Global std and Direct std are knew solar radiation spectra, which are obtained from experimental data that are inside the SPCTRAL2 model.
Conclusion
From the obtained results we can see that in the 2015 and 2017 years , the Global STD and Total spectra, do not coincide at all, this means that it has more diffuse component, and this in turn means that on the dates when the measurements were taken, maybe there were a humidity or cloudy day. However for the 2016, the Solar STD and Global spectra are very similar, this means that in the date of the measurements, were not certain humidity on the ambient and hence its verified the clear skies SPCTRAL2 model veracity. With the aid of the SPCTRAL2 model we can be able to find an approximated value for the solar irradiance received for the materials, which allow us to find the absorption and reflection coefficients with the suppositions before mentioned. Generally the absorption coefficient is a low value compared with the reflection coefficient. On the other hand, we can observe that the absorption coefficient for the dark color materials, do not have a high value, and this result does not concord with the theory prediction, this can be appreciated from the results obtained from the denim material, on this material we use just two different colors, in this results we observe that the dark color material have a very low value compared with the absorption coefficient for the blue color. We take this in account for future works.
Acknowledgment
The authors expresses sincere appreciation VIEP-BUAP for grant MOPAEXC-I, MOPA-EXC17-G, 100502999-VIEP2018, PRODEP NPTC-420 DSA/103.5/15/7449.
References
- Jacovides CP, Kaskaoutis DG, Tymvios FS (2004) Applications of SPCTRAL2 parametric model in estimating spectral solar irradiances over polluted Athens atmosphere. Renewable Energy 29: 1109-1119.
- Fred W, Billmeyer Jr (1984) Textbook of polymer science. Wiley and Sons, Inc., New York, USA.
- Shanmugan S (2013) Experimental investigation of various energy absorbing materials on performance of single slope single basin solar still with hot water provision. IJIRSET 2: 7760-7767.
- Hamza AA, Fouda IM, El-tonsy MM, El-sharkawy FM (1996) Optothermal properties of fibers, VI Effect of Annealing on some of the optical and dynamic mechanical parameters of polyester fibers. Journal of Applied Polymer Science 59: 1585-1596.
- Pomfret SJ, Adams PN, Comfort NP, Monkaman AP (1999) Advances in Processing routes for conductive polyaniline fibres. Synthetic Metals 101: 724-725
- Köppen WP (1931) Grundis der Klimakunde. Walter de Gruyter & Co. Berlín y Leipzig.
- Gusev YV (2014) On the integral law of thermal radiation. Russian Journal of Mathematical Physics 21: 460-471.
- Robert WB (1983) Radiometry and the detection of optical radiation. John Wiley & Sons, New York.
- Bird RE, Riordan C (1986) Simple solar spectral model for direct and diffuse irradiance on horizontal and tilted planes at the earth´s surface for cloudless atmospheres. J Climate Appl Meteor 25: 87-97.
- Leckner B (1978) The spectral distribution of solar radiation at the earth´s surface-elements of a model. Solar Energy 20: 143-150.
- Nann S, Riordan C (1991) Solar spectral irradiance under clear and cloudy skies: Measurement and a semiempirical model. J Appl Meteorol Climatol 30: 447-462.
- Brine DT, Iqbal M (1983) Solar Spectral diffuse irradiance under cloudless skies. Sol Energy 30: 447-453.
- Neckel H, Labs D (1981) Improved data of solar spectral irradiance from 0.33 to 1.25. Solar Phys 74: 231-249.
- National Renewable Energy Laboratory (2018) Solar resources models and tools.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi