Research Article, J Comput Eng Inf Technol Vol: 6 Issue: 6
Division of Series of Concrete Compressive Strength Results into Concrete Families in Terms of Seasons within Annual Work Period
Józef Jasiczak1*, Marcin Kanoniczak1 and ÅÂÂukasz Smaga2
1Poznan University of Technology, Piotrowo 5, 61-138 Poznan, Poland
2Adam Mickiewicz University, H. Wieniawskiego 1, 61-712 Poznan, Poland
*Corresponding Author : Prof. Dr hab. inż. Józef Jasiczak
Poznan University of Technology, Piotrowo 5, 61-138 Poznan, Poland
Tel: 61 6652494, 61 6652454, 61 6652457
E mail: jozef.jasiczak@put.poznan.pl
Received: June 24, 2017 Accepted: July 13, 2017 Published: July 20, 2017
Citation: Jasiczak J, Kanoniczak M, Smaga Å (2017) Division of Series of Concrete Compressive Strength Results into Concrete Families in Terms of Seasons within Annual Work Period. J Comput Eng Inf Technol 6:6. doi: 10.4172/2324-9307.1000187
Abstract
The basic concrete characteristic which needs to be controlled is the compressive strength of concrete, the values of which are subject to various random influences, for example climatic conditions, conditions of production and changes in the properties of components. The efficient control requires not only the registration of the decreased or increased concrete strength but also specifying the place and the date of application of concrete batch with characteristics deviating from the project assumptions. The article presents the control procedure, taking into account a division of the series of test results for the compressive strength of concrete from an annual production into concrete families of statistically stable strength parameters, in the identified time intervals. The article presents examples of verification of a hypothesis concerning the attachment of a set of compressive strength results to a concrete family, using selected statistical tests.
Keywords: Concrete family concept; Compressive strength of concrete; Control of the continuous production of concrete mix; Impact of seasonality on variability of concrete strength
Introduction
For over 100 years concrete has been the basic material used to construct roads, bridges, hydro-technical facilities, industrial buildings as well as public and residential buildings.
The specificity of these structures is that production processes are carried out in varying environmental conditions resulting both from the location of these structures in different climatic zones as well as the dynamics of concrete strength dependent on physical and mechanical processes occurring in the concrete itself.
The construction of structures have a different scope and scale, from small, individual and hence unique and one-off structures to large industrial projects with a very high consumption of concrete mix, however characterised by cyclical and multiply repeated sections. A typical example of the second group is the construction of a cement concrete motorway. In both cases, the concrete must meet the strength criteria resulting from the project requirements and applicable standards, but special focus is on mass projects which are repetitive and expensive.
Both in construction practice and theoretical considerations, particular attention is paid to ensuring that the producer can guarantee that the probability of the occurrence of the compressive strength of concrete mix is 95%.
Knowing the susceptibility of concrete shaped in the open air to a variety of environmental impacts, in the last years a lot of procedures controlling and regulating manufacturer’s compliance with limit parameters of concrete mixes, starting from statistical, global strength assessment, through range procedures (Shewart control cards), to sophisticated stochastic analysis, encompassing small range assessments of test results series with standardized, statistically significant basic parameters of the compressive strength of concrete. Verification of statistical hypotheses facilitating the identification of concrete batches forming the so-called concrete families is the subject of this article.
Impact of variable climatic and technical conditions on compressive strength of concrete
Concrete cement is an inorganic material that binds and cures as a result of a chemical reaction with water and which retains the ability to bind under water. Cements bind by hydration, thereby creating mineral compounds providing them with strength which is a fundamental parameter of the structure in use. The chemical nature of the bonds, however, causes the susceptibility of the material to any environmental impacts, including temperature, ambient relative humidity, and exposure to sunshine or wind.
Forming of structures at the construction site throughout a year on the one hand causes the structure’s exposure to time-varying impacts, which may result in periodically decreasing mechanical properties of concrete but, on the other hand, forces the contractor to maintain the projected technical parameters ensuring that the required bearing capacity is obtained. The contractor takes into account potential risks using diverse passive and effective methods. The basic knowledge is on the relationship between ambient temperature and the obtained value of the compressive strength of concrete. Figure 1 shows an example of 14 element series of the compressive strength of concrete and the corresponding series of average daily ambient temperatures.
In the analysed period of time the daily temperature decreased by 10°C, which also resulted in the decrease of the compressive strength of concrete by 20 MPa on average. Observing the trend of changes such a conclusion can be formulated quite authoritatively, however this does not mean that we deal locally with strictly additive changes. The decrease of ambient temperature associated by an increase of relative humidity of the air may even cause the increase the compressive strength of concrete, and the increase of temperature and the increase of the speed of wind can significantly reduce the strength. Therefore significant fluctuations occurred in the parameters evaluated day after day, with a general decreasing trend. High variability of individual daily average results of the tests can be observed in these trends over longer periods of time Figure 2 shows the period from July to December of a selected year, hydrotechnical structure, cube samples of 15×15×15 cm taken day after day). “Smoothing” the results by moving average method, sinusoidal behaviour of concrete strength in two-month cycles can be noticed.
Moving average y*t for a real series of the compressive strength results for concrete evaluated day after day for t-2, t and t+2 is:
 (1)
(1)
where: yi - forecasted variable yt for the period of time t,
yi - real value on the day i,
k - smoothing constant (5 was assumed for a 5-element average)
The relation is indicated by a dotted line also in Figure 2.
Here we deal not only with the climatic influences treated as local and seasonal (summer - autumn, autumn - winter etc.) but also with control processes involving the liquidation of graph extremes (variation in cement volume +/- 30 kg / m3 of the mix, the effect visible after 1 month, hence two-month cycle fluctuations can be observed). For significant climatic changes, alternative formulas of concrete mixes are adopted as shown in Table 1.
| Characteristics | Formula for the summer period | Formula for the winter period |
|---|---|---|
| Concrete class | C35/45 | C35/45 |
| Cement type | CEM I 42.5 N | CEM I 42.5 N |
| w/c | 0.44 | 0.44 |
| Sand 0 - 2 mm | 548 | 546 |
| Gravel 2 – 8 mm | 531 | 530 |
| Gravel 8 – 16 mm | 581 | 579 |
| Fly ashes | 45 | 45 |
| Plasticizer | CER – 0.25 % | - |
| Superplasticizer | O132 – 0.85 % | O146 – 0.85% |
| Aerating additive | AIR A10 – 0.15% | AIR A10 – 0.15% |
| Delaying additive | TARD – 0.30% | - |
| Accelerating additive | - | X384 -0.90% |
| Strength, 28, MPa | 52.1 | 52.7 |
Table 1: Summer and winter formulas of concrete mixes for the hydro-technical project and control data presented in Figure 2.
The differences in formulas are mainly the differences in the selection of chemical additives. In the period of high ambient temperatures the concrete mix must be artificially liquefied through the use of plasticizer and binding processes must be delayed by administering an additive flattening the kinetics of hydration heat release. At low temperatures it is the opposite: the mix must be artificially liquefied for a shorter period of time and binding processes must be accelerated, cumulating the generation of heat. In practice the formula is changed to the winter variant when the projected daily temperatures fall below + 5°C and the opposite change takes place when potentially better conditions for concrete application occur. However, in the period of low temperatures short-term warming periods may occur and thus an increase of the concrete strength takes place. Also during potentially higher temperatures rapid cooling may occur, which in turn reduces the strength. That is why the actual test results are random to a large extent.
However, the regulatory actions presented above are absolutely required for the control processes, but they should be regarded as passive actions. The effectiveness of the evaluation system can be enhanced by Total Quality Management [1] or Artificial Neural Network [2,3], or Sensitivity Analysis [4] or analysing strength characteristics in intervals, setting evaluation groups for data homogenous in an interval and analysing the so-called concrete families [5]. The last methods taken authors of this publication (Figures 3 and 4).
In the European standard EN 206-1 [6] the term of concrete family was introduced, which is defined as a group of concrete compositions for which a reliable relationship between relevant properties is established and documented, however without providing the stabilization of characteristics in any time intervals. Assignment of the individual concrete to family is closely related to the relationship between the concrete strength and technological conditions. The concept of a concrete family is presented in the relevant literature [7-10].
The determination of separate concrete families is the division of the series of test results for the compressive strength of concrete in the defined periods of time. In the continuous production of large volumes of concrete mix, appropriate estimation of a concrete family is justified from the point of view of reliability of concrete structures later in use [11-15]. The division of series of results into concrete families requires the use of appropriate statistical calculation procedures which enable the verification of statistical hypotheses assumed. Owing to this, it is possible to control the manufacturing process of concrete mix, which in turn results in the stabilization of production and obtaining the required strength parameters of concrete, as well as the desired economic effects.
Theoretical Grounds for Division of Series of Concrete Compressive Strength into Concrete Families
General assumptions
The subject of the analysis is a determined number of test results for the compressive strength of concrete, obtained by examining the strength of concrete samples taken on site during concrete application in structures.
The results of concrete strength tests are subject to the control of variability in the created subsets characteristic for the given production date of concrete mix and also to the study of variability of the entire subsets forming a certain closed number of the analysed results.
In order to determine the characteristic, maximum and average compressive strength, that is the parameters representing the whole set of the above-mentioned results, it is necessary to prepare a histogram of numerosity for this set.
Numerosity, average concrete strength and arithmetic mean of the stemplot were determined for each of the individual classes or strength ranges. Standard deviation for the whole set of results was calculated according to the following formula:
 (2)
(2)
where:
n - is the total of numerosities of all classes, ni - numerosity of class i calculated in the range of:  average value of the compressive strength of class i and x̄ - arithmetic mean of the stemplot.
average value of the compressive strength of class i and x̄ - arithmetic mean of the stemplot.
The series of numbered working plots characterising a defined volume of the concrete mix manufactured is subject to the analysis. Series  , of the results of the compressive strength tests is assigned to each plot.
, of the results of the compressive strength tests is assigned to each plot.
Verification of hypothesis concerning the attachment of test results of concrete compressive strength to a concrete family using Student’s t test
In order to compare the strength characteristics of concrete in individual subsets using Student’s t test, two random samples are compared assuming that two random samples X and Y come from a normal distribution:  respectively.
respectively.
The following set of hypothesis, referring to the expected values, is verified:
 (3)
(3)
where:  is the assumed existing expected value of probability distribution of the total set
is the assumed existing expected value of probability distribution of the total set  , where m - numerical parameter specifying the first subset of a series of compared subsets containing several individual test results of the compressive strength of concrete, r - numerical parameter specifying the number of subsets beyond the first subset in the analysed series.
, where m - numerical parameter specifying the first subset of a series of compared subsets containing several individual test results of the compressive strength of concrete, r - numerical parameter specifying the number of subsets beyond the first subset in the analysed series.
The above mentioned set of hypothesis (3) is subject to verification [16-18], which involves the analysis of strength parameters of individual subsets in the following order:
1. Checking the attachment of subsets 1 and 2 (i.e. X1 and X2) to a concrete family through verification of the set of hypotheses (3) for m = 1 and r = 0:

In the case when there is no basis for the rejection of the null hypothesis, i.e. when the subset 1 constitutes the concrete family with subset 2, one should proceed to step 2. If the null hypothesis is rejected, i.e. when subset 1 does not constitute the concrete family with subset 2, one should proceed to step 3.
2. Checking the attachment of subsets 1-2 and 3 (i.e.  and X3) to a concrete family through verification of the set of hypotheses (3) for m = 1 and r = 1:
and X3) to a concrete family through verification of the set of hypotheses (3) for m = 1 and r = 1:

In the case when there is no basis for the rejection of the null hypothesis, i.e. when subset 1-2 constitutes the concrete family with subset 3, the verification of the set of hypotheses (3) should be continued according to step 2 for m = 1and r = 2. If the null hypothesis is rejected, i.e. when the subset 1-2 does not constitute the concrete family with subset 3, one should proceed to step 3 for m = 3 and r = 0.
3. Checking the attachment of subsets 2 and 3 (i.e. X2 and X3) to a concrete family through verification of a set of hypotheses (3) for m = 2 and r = 0:

In the case when there is no basis for the rejection of the null hypothesis, i.e. when subset 2 constitute the concrete family with subset 3, one should proceed to step 2 and continue the calculation procedure for m = 2 and r = 1. If the null hypothesis is rejected, i.e. when the subset 2 does not constitute the concrete family with subset 3, the calculation procedure should be continued according to step 3 for m = 3 and r = 0.
Rejecting the null hypothesis H0 will consistently mean the adoption of the assumption that the samples come from different concrete families. However no basis for the rejection of the null hypothesis will consistently mean that the samples come from the same concrete family.
To verify the above set of hypotheses for the expected values, two different statistical tests were used, by means of which the results of two random samples were compared. Two independent random samples X and Y were analysed (representing respectively the two sets of results, each containing a specified number of the results of the concrete compressive strength tests), derived from a population of continuous distributions. In the first calculation step the sample X was the first subset of the group of all subsets analysed and the sample Y was the second subset of the group in all subsets analysed. In the second calculation step and similarly in the following steps, the sample X was a set of results representing subsets from which a concrete family was created in the previous step, and in the case when such a family could not be created, the sample X was a set of results representing the sample Y in the previous calculation step. The sample Y was always the next subset of results which was not previously used.
The study of the attachment to a concrete family using a Student’s t test for two independent samples (the analyses of the compressive strength of concrete are made independently on each of the plots) was carried out in several steps, using the strength parameters from the aforementioned subsets and from the entire set of the results of concrete compressive strength tests.
The first action was to check if the data (results) analysed come from a normal distribution. For this purpose, Shapiro-Wilk test calculations were made [19]. Next, mean values and variances were calculated from the samples X and Y. The next step was to verify the hypothesis concerning the equality of variances in two populations using equality test for two variances, i.e. test F [19]. The final essential element of the analysis was to compare the results of the two samples and to check whether they come from populations with the same expected values, using equality tests for two expected values, i.e. Student’s t test [19]. Two cases were considered. The first case in which the samples X and Y are independent and come from a normal distribution, respectively: 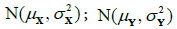 and there are equal variances for both samples
and there are equal variances for both samples  and the second case in which the samples X and Y are independent and come from a normal distribution, respectively:
and the second case in which the samples X and Y are independent and come from a normal distribution, respectively:  and there is no equality of variances of both samples
and there is no equality of variances of both samples  (also called Welch’s t test)
(also called Welch’s t test)
No basis for the rejection of the null hypothesis  given the two-sided alternative hypothesis
given the two-sided alternative hypothesis  i.e. where:
i.e. where:  for the first case or
for the first case or for the second case mean the adoption of the hypothesis on the attachment of the group of results, representing samples X and Y, to one concrete family. However, if the null hypothesis is rejected, i.e. if for the first case
for the second case mean the adoption of the hypothesis on the attachment of the group of results, representing samples X and Y, to one concrete family. However, if the null hypothesis is rejected, i.e. if for the first case  or where
or where  for the second case, then the hypothesis on the attachment of the group of results, representing samples X and Y, to one concrete family is rejected.
for the second case, then the hypothesis on the attachment of the group of results, representing samples X and Y, to one concrete family is rejected.
Verification of hypothesis concerning the attachment of test results of concrete compressive strength to a concrete family using Mann – Whitney U-test
The study of the attachment to a concrete family consists in a verification of a set of hypothesis on the equality of distribution functions of two samples distribution:
 (4)
(4)
where:  is the distribution function of the probability of “total” sample
is the distribution function of the probability of “total” sample  The set of hypothesis (4) is subject to verification in the same manner as the set of hypothesis (3) but using the Mann – Whitney U - test [19].
The set of hypothesis (4) is subject to verification in the same manner as the set of hypothesis (3) but using the Mann – Whitney U - test [19].
The null hypothesis H0 assumes that samples X and Y were taken from the same distribution and the alternative hypothesis H1 assumes that samples X and Y were not taken from the same distribution.
The study of attachment to a concrete family by Mann – Whitney U-test for two independent samples is carried out taking into consideration two sets from which two independent samples X and Y are taken at random. All observations are subject to sorting in the rising order. In the case when two identical observations are made in samples X and Y a correction should be applied by adding to the U statistics value a half of the number of pairs (x, y) such that x = y. No basis for the rejection of the null hypothesis  given the two-sided alternative
given the two-sided alternative where U(X, Y) does not belong to the set
where U(X, Y) does not belong to the set means the adoption of the hypothesis with the attachment of the group of results representing samples X and Y to one concrete family. However, if the null hypothesis is rejected, i.e. where: U(X, Y) belongs to the set
means the adoption of the hypothesis with the attachment of the group of results representing samples X and Y to one concrete family. However, if the null hypothesis is rejected, i.e. where: U(X, Y) belongs to the set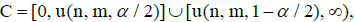 it means that the hypothesis on the attachment of the group of results representing samples X and Y to one concrete family is rejected.
it means that the hypothesis on the attachment of the group of results representing samples X and Y to one concrete family is rejected.
Examples of Calculations
Analysis of annual set of test results for the compressive strength of concrete
In order to determine the strength characteristics of an annual set of test results for the compressive strength of concrete a numerosity histogram was used. Parameters representing the whole set of data were obtained, without their correlation with the time of production of the concrete mix.
Analysing the series of individual compressive strength tests, a significant variability of the compressive strength can be noticed. The entire set of test results has an average compressive strength of 53.1 MPa, standard deviation is 3.6 MPa and the characteristic strength is fck = 47.2 MPa, higher than fck = 45.0 MPa assumed at the beginning, but belonging to the same projected concrete class C35/45.
Division of the series of compressive strength results into concrete families
The assumptions of hypothesis (3) and (4) on the attachment of the set of concrete strength test results to a concrete family using Student’s t test and Mann – Whitney U-test were verified according to the calculation procedure presented in section 3. Using the first test method, the division of the entire set of results into 68 concrete families was obtained and in the second test the division of the entire set of results into 71 concrete families was achieved. Figure 4 shows the basic data referring to the series of test results, the corresponding standard deviations and ranges of statistically stable parameters determined by verification of statistical hypothesis using Student’s t test and Mann – Whitney U-test. The results of the hypotheses verification for the beginning of the test results series are provided in Tables 2 and 3. Table 4 shows the result of verification calculations performed. The table provides compressive strength characteristics for individual concrete families separated from 45 subsets comprised by the set of annual results.
| Item | Range | n1 | n2 | Statistics value of Student’s t test | n1 + n2 or βr | Value of statistics quantile of Student’s t test (α=0.05) |
Attachment to concrete family |
|---|---|---|---|---|---|---|---|
| 1 | 1 -2 | 5 | 6 | 4,38 | 9 | 2,26 | Does not belong to concrete family |
| 2 | 2 - 3 | 6 | 7 | 1,43 | 11 | 2,20 | Belongs to concrete family |
| 3 | 2 - 4 | 13 | 7 | 0,36 | 18 | 2,10 | Belongs to concrete family |
| 4 | 2 - 5 | 20 | 7 | - 3,77 | 25 | 2,06 | Does not belong to concrete family |
| 5 | 5 - 6 | 7 | 7 | - 2,89 | 12 | 2,18 | Does not belong to concrete family |
| 6 | 6 - 7 | 7 | 7 | - 2,49 | 12 | 2,18 | Does not belong to concrete family |
| 7 | 7 - 8 | 7 | 8 | 4,63 | 13 | 2,16 | Does not belong to concrete family |
| 8 | 8 - 9 | 8 | 7 | - 1,75 | 13 | 2,16 | Belongs to concrete family |
| 9 | 8- 10 | 15 | 8 | - 5,58 | 21 | 2,08 | Does not belong to concrete family |
| 10 | 10 - 11 | 8 | 8 | 0,70 | 14 | 2,14 | Belongs to concrete family |
| 11 | 10 - 12 | 16 | 5 | - 1,29 | 18,72 | 2,10 | Belongs to concrete family |
| 12 | 10 -13 | 21 | 5 | 1,42 | 24 | 2,06 | Belongs to concrete family |
| 13 | 10 - 14 | 26 | 5 | 7,77 | 29 | 2,05 | Does not belong to concrete family |
| 14 | 14 - 15 | 5 | 7 | - 8,23 | 10 | 2,23 | Does not belong to concrete family |
| 15 | 15 - 16 | 7 | 5 | 7,19 | 10 | 2,23 | Does not belong to concrete family |
| 16 | 16 - 17 | 5 | 5 | - 1,56 | 8 | 2,31 | Belongs to concrete family |
| 17 | 16 - 18 | 10 | 6 | 1,60 | 14 | 2,15 | Belongs to concrete family |
| 18 | 16 - 19 | 16 | 5 | - 7,65 | 19 | 2,09 | Does not belong to concrete family |
| 19 | 19 - 20 | 5 | 7 | - 1,22 | 10 | 2,23 | Belongs to concrete family |
| 20 | 19 - 21 | 12 | 5 | 9,22 | 15 | 2,13 | Does not belong to concrete family |
Table 2: Results of verification of hypotheses concerning attachment to concrete families using Student’s t test (subsets 1 – 21).
| 1 | 1 – 2 | 5 | 6 | 2,0 | < 0 ; 4 > u < 26 ; ∞ ) | Does not belong to concrete family |
| 2 | 2 – 3 | 6 | 7 | 13,5 | < 0 ; 7 > u < 35 ; ∞ ) | Belongs to concrete family |
| 3 | 2 – 4 | 13 | 7 | 45,5 | < 0 ; 21 > u < 70 ; ∞ ) | Belongs to concrete family |
| 4 | 2 – 5 | 20 | 7 | 127,0 | < 0 ; 35 > u < 105 ; ∞ ) | Does not belong to concrete family |
| 5 | 5 – 6 | 7 | 7 | 41,5 | < 0 ; 9 > u < 40 ; ∞ ) | Does not belong to concrete family |
| 6 | 6 – 7 | 7 | 7 | 39,0 | < 0 ; 9 > u < 40 ; ∞ ) | Belongs to concrete family |
| 7 | 6 – 8 | 14 | 8 | 9,0 | < 0 ; 27 > u < 85 ; ∞ ) | Does not belong to concrete family |
| 8 | 8 – 9 | 8 | 7 | 39,0 | < 0 ; 11 > u < 45 ; ∞ ) | Belongs to concrete family |
| 9 | 8 – 10 | 15 | 8 | 116,0 | < 0 ; 30 > u < 90 ; ∞ ) | Does not belong to concrete family |
| 10 | 10 – 11 | 8 | 8 | 27,5 | < 0 ; 14 > u < 50 ; ∞ ) | Belongs to concrete family |
| 11 | 10 – 12 | 16 | 5 | 51,5 | < 0 ; 16 > u < 64 ; ∞ ) | Belongs to concrete family |
| 12 | 10 – 13 | 21 | 5 | 28,0 | < 0 ; 23 > u < 82 ; ∞ ) | Belongs to concrete family |
| 13 | 10 – 14 | 26 | 5 | 0 | < 0 ; 29 > u < 101 ; ∞ ) | Does not belong to concrete family |
| 14 | 14 – 15 | 5 | 7 | 35,0 | < 0 ; 6 > u < 29 ; ∞ ) | Does not belong to concrete family |
| 15 | 15 – 16 | 7 | 5 | 0 | < 0 ; 6 > u < 29 ; ∞ ) | Does not belong to concrete family |
| 16 | 16 – 17 | 5 | 5 | 17,0 | < 0 ; 3 > u < 22 ; ∞ ) | Belongs to concrete family |
| 17 | 16 – 18 | 10 | 6 | 11,5 | < 0 ; 12 > u < 48 ; ∞ ) | Does not belong to concrete family |
| 18 | 18 – 19 | 6 | 5 | 30,0 | < 0 ; 4 > u < 26 ; ∞ ) | Does not belong to concrete family |
| 19 | 19 – 20 | 5 | 7 | 26,0 | < 0 ; 6 > u < 29 ; ∞ ) | Belongs to concrete family |
| 20 | 19 – 21 | 12 | 5 | 0 | < 0 ; 12 > u < 48 ; ∞ ) | Does not belong to concrete family |
Table 3: Results of verification of hypotheses concerning attachment to concrete family using Mann - Whitney U-test (subsets 1 – 21).
| Projected characteristic compressive strength of concrete fck = 45.0 MPa | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entire set of test results for compressive strength of concrete | Numerosity of subset | 719 | ||||||||||||||
| Average compressive strength | 53,1 | |||||||||||||||
| Standard deviation | 3,6 | |||||||||||||||
| Calculated characteristic compressive strength | 47,2 | |||||||||||||||
| Concrete class C | 35/45 | |||||||||||||||
| Division into concrete families | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| Division by Student’s t test | Numerosity of subset | 5 | 20 | 7 | 7 | 7 | 15 | 26 | 5 | 7 | ||||||
| Average compressive strength | 55.4 | 50.3 | 52.9 | 56.1 | 62.0 | 52.5 | 58.8 | 50.0 | 60.3 | |||||||
| Standard deviation | 1.7 | 1.9 | 1.1 | 2.5 | 5.7 | 2.9 | 2.6 | 1.4 | 2.4 | |||||||
| Calculated characteristic compressive strength | 52.6 | 47.2 | 51.1 | 52.0 | 52.7 | 47.7 | 54.6 | 47.7 | 56.3 | |||||||
| Concrete class C | 40 /50 |
35/45 | 40 /50 |
40 /50 |
40 /50 |
35/45 | 40/50 | 35 /45 |
45 /55 |
|||||||
| Division by Mann - Whitney U -test |
Numerosity of subset | 5 | 20 | 7 | 14 | 15 | 26 | 5 | 7 | |||||||
| Average compressive strength | 55.4 | 50.3 | 52.9 | 59.0 | 52.5 | 58.8 | 50.0 | 60.3 | ||||||||
| Standard deviation | 1.7 | 1.9 | 1.1 | 5.1 | 2.9 | 2.6 | 1.4 | 2.4 | ||||||||
| Calculated characteristic compressive strength | 52.6 | 47.2 | 51.1 | 50.5 | 47.7 | 54.6 | 47.7 | 56.3 | ||||||||
| Concrete class C | 40 /50 |
35/45 | 40 /50 |
40/50 | 35/45 | 40/50 | 35 /45 |
45 /55 |
||||||||
| Division into concrete families – continuation | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| Division by Student’s t test | Numerosity of subset | 16 | 12 | 10 | 17 | 10 | 5 | 5 | 5 | |||||||
| Average compressive strength | 51,5 | 56,8 | 49,6 | 54,3 | 61,2 | 54,0 | 57,2 | 53,4 | ||||||||
| Standard deviation | 1,2 | 2,0 | 1,0 | 3,0 | 3,3 | 0 | 1,1 | 0,9 | ||||||||
| Calculated characteristic compressive strength | 49,6 | 53,6 | 48,0 | 49,4 | 55,8 | 54,0 | 55,4 | 51,9 | ||||||||
| Concrete class C | 35/45 | 40/50 | 35/45 | 35/45 | 45/55 | 40 /50 |
45 /55 |
40 /50 |
||||||||
| Division by Mann - Whitney U -test |
Numerosity of subset | 10 | 6 | 12 | 10 | 17 | 10 | 5 | 5 | 5 | ||||||
| Average compressive strength | 51,8 | 51,0 | 56,8 | 49,6 | 54,3 | 61,2 | 54,0 | 57,2 | 53,4 | |||||||
| Standard deviation | 1,1 | 1,1 | 2,0 | 1,0 | 3,0 | 3,3 | 0 | 1,1 | 0,9 | |||||||
| Calculated characteristic compressive strength | 49,9 | 49,2 | 53,6 | 48,0 | 49,4 | 55,7 | 54,0 | 55,4 | 51,9 | |||||||
| Concrete class C | 35/45 | 35 /45 |
40/50 | 35/45 | 35/45 | 45/55 | 40 /50 |
45 /55 |
40 /50 |
|||||||
| Division into concrete families – continuation | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | |
| Division by Student’s t test | Numerosity of subset | 10 | 5 | 15 | 11 | 10 | 5 | 10 | 12 | |||||||
| Average compressive strength | 56,2 | 54,0 | 49,6 | 52,5 | 50,4 | 57,6 | 54,6 | 59,2 | ||||||||
| Standard deviation | 1,4 | 0 | 1,7 | 2,0 | 1,0 | 1,7 | 1,6 | 2,0 | ||||||||
| Calculated characteristic compressive strength | 53,9 | 54,0 | 46,8 | 49,2 | 48,8 | 54,8 | 52,0 | 55,9 | ||||||||
| Concrete class C | 40/50 | 40 /50 |
35/45 | 35/45 | 35/45 | 40 /50 |
40/50 | 45/55 | ||||||||
| Division by Mann - Whitney U -test |
Numerosity of subset | 10 | 5 | 15 | 5 | 6 | 10 | 5 | 5 | 5 | 12 | |||||
| Average compressive strength | 56,2 | 54,0 | 49,6 | 51,6 | 53,7 | 50,4 | 57,6 | 53,8 | 55,2 | 59,2 | ||||||
| Standard deviation | 1,4 | 0 | 1,7 | 0,9 | 1,6 | 1,0 | 1,7 | 1,1 | 1,1 | 2,0 | ||||||
| Calculated characteristic compressive strength | 53,9 | 54,0 | 46,8 | 50,1 | 51,0 | 48,8 | 54,8 | 52,0 | 53,4 | 55,9 | ||||||
| Concrete class C | 40/50 | 40 /50 |
35/45 | 40 /50 |
40 /50 |
35/45 | 40 /50 |
40 /50 |
40 /50 |
45/55 | ||||||
Table 4: Concrete strength characteristics in concrete families identified from 45 subsets comprised by an annual set of results.
Conclusions and Summary
• The continuous production of concrete mix requires ongoing monitoring. The main parameter subject to this control is the compressive strength of concrete. This strength is tested on samples taken from systematically collected amounts of the mixture at a fixed time of production. Next, the set of results achieved is subject to analysis. The annual set of test results of the compressive strength of concrete can be assessed globally, with respect to strength parameters representing all results from the set obtained. However, the analysis of all the results in the set does not allow the detection of decreased or excessively increased concrete strength values which may occur in certain periods of production.
• Analysing the strength parameters of individual concrete families obtained from the division of the annual set of results for the compressive strength of concrete by means of Student’s t test and Mann - Whitney U-test, a significant variability of the characteristic strength can be noticed. For 25 concrete families established as a result of the division by means of Student’s t test of the set of results representing 45 subsets (about 1/3 of subsets included in the entire set of results), as many as 16 concrete families show higher characteristic compressive strength of concrete than the characteristic compressive strength of the entire set of results (12 concrete families represent concrete class C40 / 50 and 4 families represent class C45 / 55). The remaining 9 families represent the concrete class assumed at the beginning, i.e. C35 / 45.
However, for 27 concrete families established as a result of the division, by means of Mann - Whitney U-test, of the set of results representing the same 45 subsets, as many as 18 families show higher characteristic concrete strength than the compressive strength characteristic for the annual set of results (14 families represents concrete class C40 / 50 and 4 families represent concrete class C45 / 55). The remaining 9 families represent the concrete class assumed at the beginning, i.e. C35 / 45. These results clearly indicate the existence of the compressive strength instability in the whole set of results. Locally, at certain intervals, excessive strength occurs, significantly exceeding the projected concrete class. This is an error on the safe side, but it means an increase of outlays associated with the production of concrete with higher compressive strength range, unnecessary from the point of view of the structure safety (instead of class C35 / 45, the achieved class is C40 / 50 and C45 / 55). The popular passive control can ensure the structure safety, but in an economically inefficient manner.
• The system’s efficiency can be considerably improved by considering concrete families in details, implementing active control assessment based on the verification of statistical hypotheses described in the article. The analysis of the compressive strength of concrete produced at a certain time of production, represented by a group of results characterizing the statistical invariability of parameters, i.e. belonging to one concrete family, allows the detection of an element (group of elements) with inadequate strength characteristics. This is fully justified from the point of view of structural reliability and economic optimization of the production of concrete mix.
References
- Kumar S, Mantha SS, Kumar A (2009) Scrap reduction by using total quality management tools. Int J Ind Eng 16: 364-369
- Young WA, Weckman GR, Brown MD, Thompson J (2008) Extracting knowledge of concrete shear strength from artificial neural networks. Int J Ind Eng 15: 26-35.
- Young WA, Weckman GR, Brown MD, Thompson J (2008) Extracting knowledge of concrete shear strength from artificial neural networks. Int J Ind Eng 15: 26-35.
- Shamsipoor H, Sandidzadeh MA, Yaghini M (2012) Solving capacitated P-median problem by a new structure of neural network. Int J Ind Eng 19: 305-319.
- Teng HM, Chiu Y, Hsu PH, Wee HM (2012) An analytical approach of sensitivity analysis for EOQ. Int J Ind Eng19: 204-212.
- Jasiczak J (2011) Probabilistic criteria for the control of compressive strength stabilization in concrete. FCEE 14: 47-61.
- EN 206-1: 2000 Concrete. Part 1: Specification, performance, production and conformity.
- Caspeele R, Taerwe L (2007) Conformity Control of Concrete Based on the “Concrete Family” Concept. Beton-und Stahlbetonbau 103: 50-56.
- Concrete according to PN-EN 206-1 standard – comments – collective work under the guidance of Lech Czarnecki. (2004) Polski Cement, Kraków, Czech Republic.
- Kohutek Z (2010) Concrete Family – the genesis of concept, terminology, criteria, General Principles of Creation. PrzeglÄ…d Budowlany 10: 26-31.
- Ping LJ, Hong SG, Yong GL (2010) Use of “Concrete Family” Concept for Conformity Control of Ready Mixed Concrete. 35th conference on our world in concrete & structures, Singapore.
- Reported by ACI Committee 214 (2011) ACI 214R-11 Guide to Evaluation of Strength Test Results of Concrete.
- Reported by ACI Committee 318 (2008) Building Code Requirements for Structural Concrete (ACI 318-08) and Commentry. An ACI Standard.
- EN 1992:2008 Eurocode 2: Design of Concrete Structures.
- ISO 2394:2000 General Principles on Reliability for Structures.
- Sarja A (2000) Durability Design of Concrete Structures – Committee Report 130-CSL. Mater Struct 33: 14-20.
- Jasiczak J, Kanoniczak M, Smaga Å (2014) Standard term concrete families on the example of continuous production of spiroll boards. Construction and architecture Budownictwo i Architektura 13: 99-108.
- Jasiczak J, Kanoniczak M, Smaga Å (2015) Stochastic identity of test result series of the compressive strength of concrete in industrial production conditions. Arch civ mech eng 15: 584-592.
- Górecki T (2011) Basics of the statistics with examples in R. BTC, Legionowo (in Polish).
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi