Research Article, J Comput Eng Inf Technol Vol: 11 Issue: 10
Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Parameter Calibration in Hydrological Simulation
Xinyu Zhang* and Yang Li
Department of Science and Technology, University of Science and Technology Beijing, Beijing, China
*Corresponding Author: Xinyu Zhang, Oncology Clinic, Department of Science and Technology, University of Science and Technology Beijing, Beijing, China, Tel: +18611590131; E-mail: xy_zhangzhang@foxmail.com
Received date: 26 July, 2022, Manuscript No. JCEIT-22-70423; Editor assigned date: 29 July, 2022, PreQC No. JCEIT-22-70423 (PQ); Reviewed date: 12 August, 2022, QC No. JCEIT-22-70423; Revised date: 03 October, 2022, Manuscript No. JCEIT-22-70423 (R); Published date: 10 October, 2022, DOI:10.4172/2324-9307.1000254
Citation:Zhang X, Li Y (2022) Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Parameter Calibration in Hydrological Simulation. J Comput Eng Inf Technol 11:10.
Abstract
Parameter calibration is an important part of hydrological simulation and affects the final simulation results. In this paper, we introduce heuristic optimization algorithms, Genetic Algorithm (GA) and Particle Swarm Optimization Algorithm (PSO), to cope with the complexity of the parameter calibration problem. In large scale hydrological simulations, we use a multilevel parallel parameter calibration algorithm framework to make full use of processor resources and accelerate the process of solving high dimensional parameter calibration. The results of parameter calibration with GA and PSO can basically reach the ideal value of 0.65 and above, with PSO achieving a speedup of 7.67 on TianHe-2 supercomputer. The experimental results indicate that by using a parallel implementation on multicore CPUs, high dimensional parameter calibration in large scale hydrological simulation is possible. Moreover, our comparison of the two algorithms shows that the GA obtains better calibration results and the PSO has a more pronounced acceleration effect.
Keywords: Hydrologic simulation, Parameter calibration, Genetic algorithm, Particle swarm optimization
Introduction
Hydrological models are widely used in many fields such as drought forecasting, flood protection and water resources management systems [1-4]. The results of hydrological simulations depend to a large extent on the merits of the model parameters. The process parameters in the hydrological model must be calibrated. Parameter calibration of hydrological model is an important process in which parameter adjustment are made so as to match (as closely as possible) to the actual observed values. However, in complex practical applications, due to the high complexity of the hydrological process, the simulation of a large range of watersheds, the need to calibrate more parameters, traditional optimization methods often suffer from computational dimensionality curse. In addition, due to the long time consumption of the serial execution of the parameter calibration process, the excessively slow calibration speed seriously reduces the efficiency.
There are two types of parameter calibration methods; manual trial and error method and automatic calibration method. The trial and error method requires manually adjusting parameters to match the simulated results with observed values, while the method not only takes a long time to debug, but also depends on the human experience, which increases the uncertainty of the model. The automatic calibrations involve with setting up objective functions, developing optimization algorithms and setting up termination conditions as calibration targets [5].
Traditional optimization algorithms, such as the gradient method and Newton method, are susceptible to local convergence by initial values and often fail to obtain globally optimal solutions, resulting in strong instability of optimization results impossible to be promoted in practical applications [6-9]. Since the 1980's, modern optimization algorithms, mainly including Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Shuffled Complex Evolution Algorithm (SCE-UA), Simulated Annealing Algorithms (SAA) and Artificial Neural Networks (ANN), have emerged and greatly promoted the development of parameter optimization of hydrological models [10-13]. However, the model parameters calibration using modern optimization methods needs to carry out an efficient and sufficient search of the parameter sets by evaluating a large set of parameters to determine the optimal solution, which is usually computationally intensive, consumes many system resources and causes a huge computational burden [14]. With the rapid development of high performance computing, parallel computing has become an effective means to improve the efficiency of large-scale data processing and combining optimization algorithms with parallelism can further improve the feasibility [15-17]. In terms of specific practical applications with optimization problems of high dimensionality and complexity, the curse of dimensionality causes slow convergence of the solution for parameters optimization and the individuals makes the search easily fall into local optimal in the optimization process. In addition, the parallelization for calibrating hydrologic models requires load balancing and communication minimization.
In this paper, we use two heuristic algorithms to calibrate parameters of hydrologic models in large scale. There are three main contributions of our research work. First, we propose a multi-level parallel parameter calibration algorithm framework, where the inner parallel layer implements water cycle simulation and the outer parallel layer manipulates parameter iteration and optimization search by dividing sub domains. In our case, we use the GA and the PSO to calibrate parameters. Second, we propose a technique to parallelize both the GA and the PSO while minimizing the communication between the processes in order to make full use of computing resources with multicore CPUs. Finally, we compare the feasibility and parallel efficiency of the set of parameters generated by our GA based and PSO based parameter calibration. The results given in this paper clearly illustrate that parallel GA is suitable for applications requiring high calibration accuracy, parallel PSO is suitable for applications with fast calibration response.
Materials and Methods
The remainder of this paper is organized as follows. The next section discusses the related work. Then we present the multi-level parallel parameter calibration framework we applied in large scale hydrologic simulation, followed using the GA and the PSO to calibrate parameters in hydrologic models. Finally, we present the parallel implementation of the GA and the PSO in order to allow parameter calibration in large scale and compare the validation and performances of calibration results produced by the GA and the PSO and summarize the conclusion.
Related work
Parameter calibration is an important part that affects the accuracy and efficient in large-scale hydrological simulation. The traditional parameter calibration method mainly adopts the manual experiment method, that is, a set of parameters is randomly selected from a given parameter range and then the selected parameters are used to simulate [18]. Due to the large number and range of parameters, thousands of calculations are required during the calibration process. The obvious disadvantage of manual methods is that they consume much time and energy.
There are optimization algorithms used to calibrate hydrologic models such as Gauss-Newton type methods, Shuffled Complex Evolution of the University of Arizona (SCEUA), Particle Swarm Optimization (PSO), Genetic Algorithm (GA) and Artificial Neural Networks (ANN) [19-23]. Gauss-Newton type algorithm as local calibration methods for the optimization of hydrological models, it is usually more robust while keeping costs down but tend to get trapped in a local optimum when solving multiextreme value problems. More efficient global optimization algorithms are proposed to consistently locate the global optimum of the hydrological models. The SCE-UA was used to calibrate in a complex watershed model and the recommended values for the SCE-UA can be construed as guidelines for most application. GA and PSO as optimization algorithms based on the natural intelligence of the biological world, both algorithms have been widely used for parameter calibration of hydrological models [24,25]. The parameters of the Muskingum model which are calibrated by the particle swarm algorithm are applied to the Yalong river basin in 2013. Wang earlier proposed to apply the GA to the parameter calibration of flow in a runoff model. Cheng combined GA with the fuzzy optimal model and applied it to the parameter calibration of Xinanjiang model. The Bayesian approach was applied to the Nash-Cascade model and Sacramento model. The authors used the Leaf River basin in Mississippi as an example and verified that the Bayesian recursive estimation algorithm has good results in parameter optimization. However, these parameter optimization methods are executed serially, which can be time-consuming when applied to large scale simulation. With the development of hydrological simulation combined with parallel technology, Kollet demonstrated the correctness and feasibility of using parallel computing for hydrological simulation. Yalew, explored the use of parallel computing for hydrological simulation in Soil and Water Assessment Tool (SWAT). A master slave dynamic task assignment scheduling strategy was proposed to parallelize hydrological simulation by Li. Despite the introduction of parallel techniques and the corresponding improvement in the computational efficiency of hydrological models, these studies are aimed at the accelerated solution of the computational process of hydrological simulation and do not directly accelerate the process of parameter calibration. Rouholahnejad, parallelized the calibration of the SWAT hydrological model. And, a parallel optimization algorithms Multi-core Parallel Artificial Bee Colony algorithm (MPABC) was proposed to improve the optimization precision and performance for parameters optimization of the Xinanjiang model. A Multicore Parallel Genetic Algorithm (MCPGA) based on the fork join parallel framework proposed is also applied to parameter calibration for the Xinanjiang model.
These studies have used multicore parallel technology to offer considerable benefits for parameter calibration, but most of their methods focus on improving optimization algorithms and not many are based on parallel frameworks.
Multi-level parallel parameter calibration
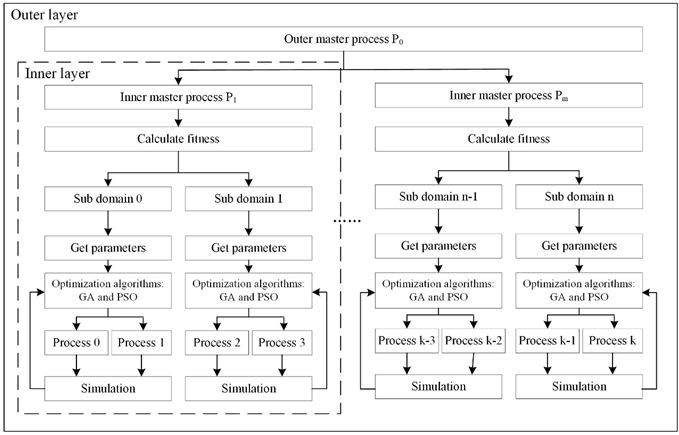
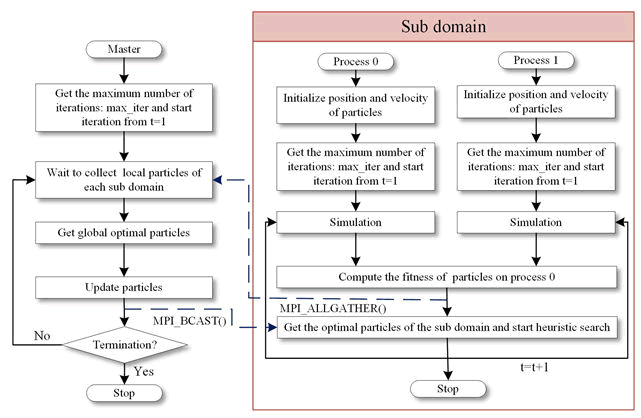
In order to meet the need for parameter optimization in large scale and better improve the computational efficiency, we introduce multilevel parallelism, with the inner layer, processes within each sub domain, using a custom message queue data structure and introducing parallelism in two dimensions of space time for water cycle simulation; the outer layer, between sub domains, using Message Passing Interface (MPI) to divide the sub domain based on the masterslave model to parallelize the optimization space. The multilevel parallel parameter calibration algorithm framework is shown in Figure 1.
Figure 1: Multilevel parallel parameter calibration algorithm framework. The main process in the outer layer divides the currently idle processes into several inner parallel communication domains and all processes in each inner parallel communication domain execute the parameter calibration tasks in parallel.
MPI is a parallel program interface with good performance. It has two most basic parallel program design modes; peer to peer mode and master slave mode. In our work, the parameter calibration is based on the master slave mode to realize parallelism. In this master slave mode, we add a layer of internal master processes to the parallel framework, where the slave processes in each sub domains will first send the corresponding results to the internal master process, which will then perform the corresponding calculations and finally send the results to the external master process. Each internal master process is responsible for the communication of several adjacent sub domains, which effectively reduces the communication consumption of the outer master process and further accelerates parameter calibration process.
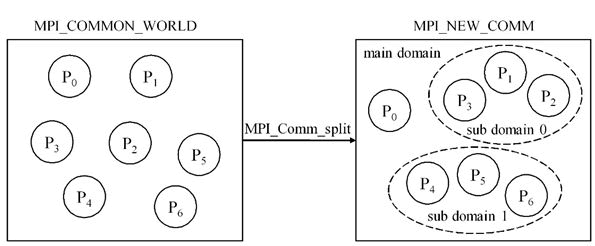
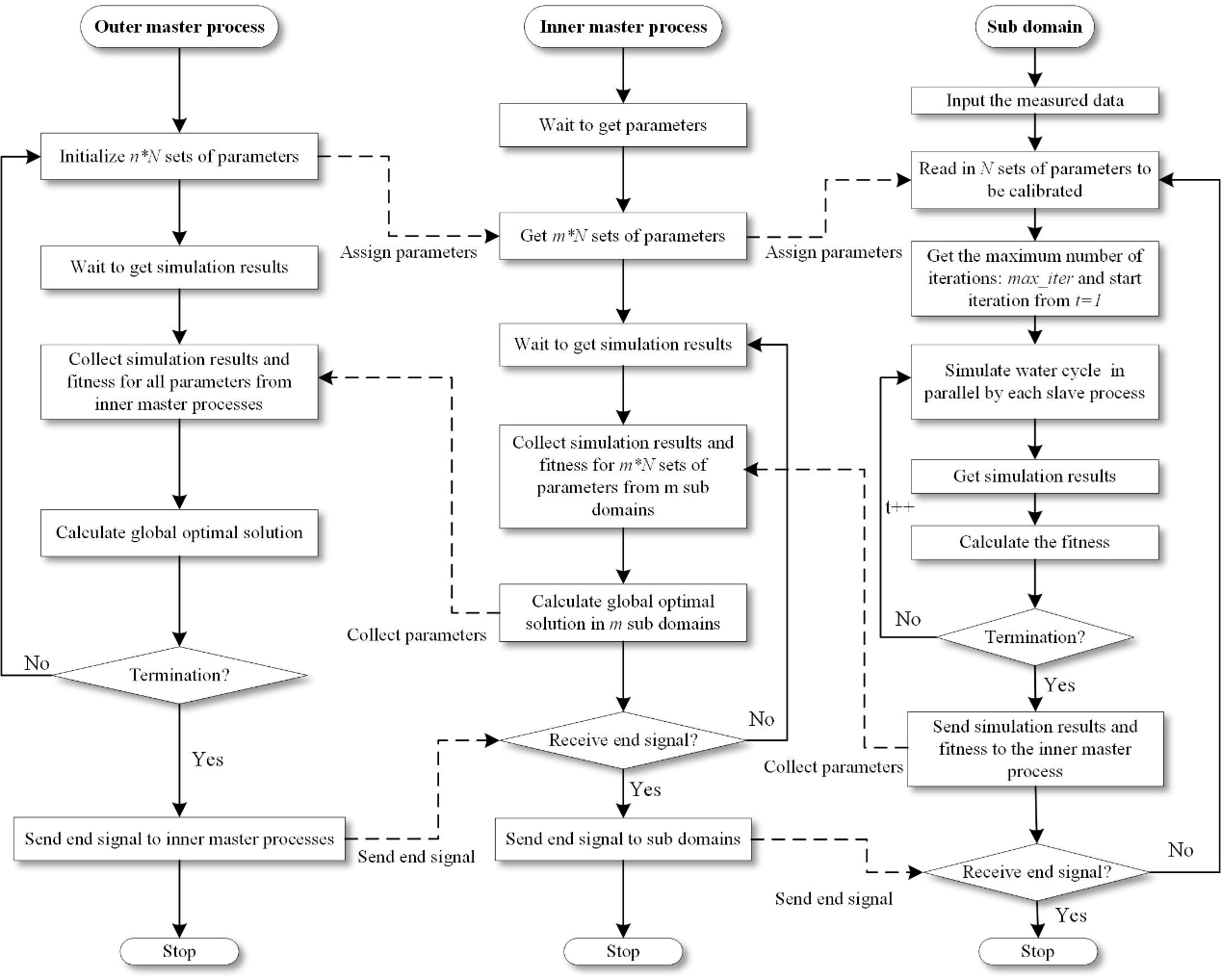
We will focus on the parallel parameter calibration part in the outer layer. The way to divide the sub domain through the MPI is shown in Figure 2. The whole communication domain MPI_COMM_WORLD is divided into a new communication domain MPI_NEW_COMM by MPI_Comm_split, where process p0 is divided into a separate main domain and the rest of the processes form multiple sub domains. The multilevel parallel parameter calibration flowchart is shown in Figure 3. First, sub domains obtain N sets of parameters and perform the water cycle simulation. And then the simulation results are compared with corresponding measured values and these results as well as the parameters are recorded in each iteration. When sub domain has completed all the iterations, they send the above data to the inner master process in its own sub domain respectively and the inner master process is responsible for calculating the optimal solutions and sending them to the external master process. The simulation results are further passed to the external master process for the final calibration. It is worth noting that we introduce GA and PSO to accelerate the optimization in the part of parameter calibration.
Figure 2: A domain divided into two sub domains. The domain consisting of 7 processes in the figure called MPI_COMM_WORLD, where each circle represents a process. The domain divided into two sub domains by MPI_Comm_split. The new domain called MPI_NEW_COMM, where process P0 is divided into a separate main domain, p1, p2 and p3 form sub domain 0 and p4, p5 and p6 form sub domain 1.
For hydrological simulation, the measurement standard representing the hydrological simulation index can be used as a fitness function, such as the Nash-Sutcliffe Efficiency (NSE) or the determination coefficient (R2). The specific formula for calculating the NSE and R2 are defined as follows:
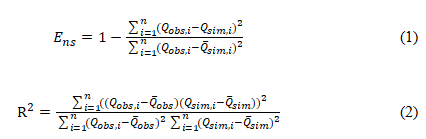
Where Qobs,i is the observed value of the ith sub-basin and Qsim,i is the simulated value of the ith sub-basin. The NSE, also known as the simulation efficiency coefficient, takes a value range of -∞ to 1. If the NSE close to 1, the simulation quality is good; close to 0, the overall results are credible simulation process error is large; much less than 0, the model is not credible. The coefficient of determination R2 takes value of 0.0 to 1.0 and the ideal value is 0.8 to 1.0. The R2 closer to 1 means that the difference between the simulated runoff and the measured runoff is smaller.
Parallel Genetic Algorithm (PGA
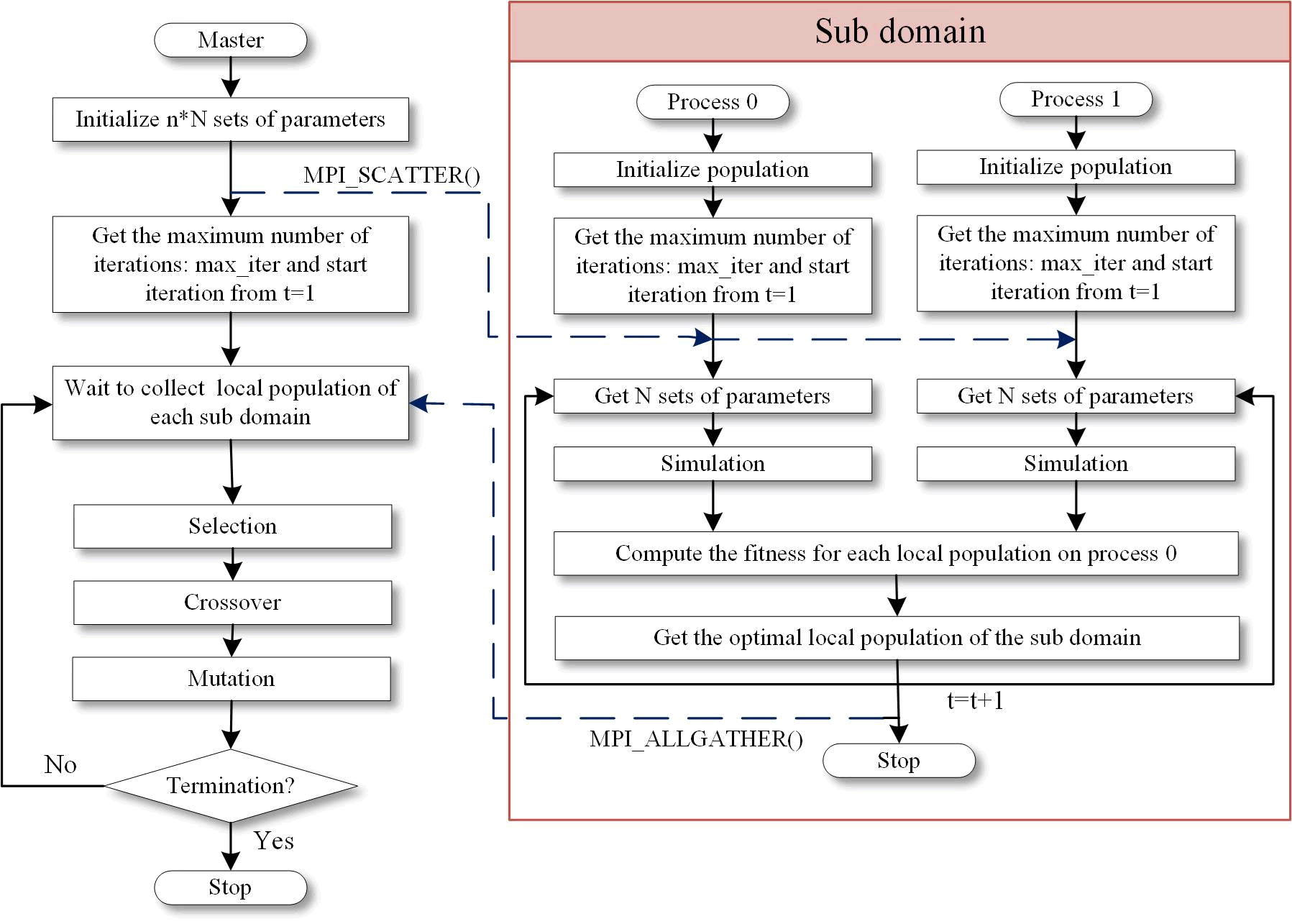
The GA is an adaptive heuristic search algorithm based on the evolutionary process of natural selection and genetic. The GA simulates the evolution process of the natural population and selects the optimal individual which adapts to the environment by eliminating backward genes and the solution of the optimization problem can be regarded as a set of chromosomes. In recent years, the GA has been used for calibration of conceptual runoff model and optimization of cascade stilling. As the scale of optimization problem increases and the search space becomes more complex, with the GA inherent parallelism, Parallel Genetic Algorithm (PGA) becomes the most significant way to solve these complicated problems efficiently and effectively. In this work, we use master slave PGA to simulate the evolution of a population with multiple sets of parameters in hydrological simulation adapting to the objective function.
The flowchart of our parallel GA is displayed in Figure 4.
In our implementation, a set of parameters of the sub-basins is a set of chromosomes and a specific parameter value on the chromosome represents a gene. The essence of GA is to obtain the optimal solution that satisfies the condition by changing the value of the gene. The flowchart of the GA includes chromosome selection, crossover and mutation. The initial population with multiple sets of parameters is randomly generated within the set parameter value range. The chromosome selection is mainly based on the roulette wheel selection to ensure randomness and the selection criterion is the fitness of the solution that refers to the objective function we ultimately need to solve. The fitness evaluation of individuals is assigned to different processors. In our hydrological simulation, we take R2 coefficient as the fitness. The serial operation of selection consists of the following steps. First, the R2 coefficient of N sets of parameters for water cycle simulation are calculated and the probability of each set of parameters being inherited to the next generation population can be calculated by:

Where P (Xi) is the inheritance probability of the ith chromosome, f (xi) is the R2 coefficient of the ith chromosome. The inheritance probability of each chromosome is then be accumulated. Second, a uniformly distributed value is randomly generated in (0,1), if the value is less than the cumulative probability of the first chromosome, the first chromosome can be selected and if the value is between the cumulative probability of two chromosomes, the latter chromosome is selected. N chromosomes, that are N sets of the parameters, can be selected repeating the above steps N times
When the parents are selected, children can be created from parents using single point crossover. Significantly, if the number of chromosomes is odd, the last chromosome is directly retained. The children solutions need to mutate to guarantee the diversity of the population and avoid the local convergence caused by the crossover.
According to the number of parameters in the current sub-basins, mutation points are randomly set for the chromosomes and the value at the mutation point should be set within the value range given in the parameter configuration file. Finally, the optimal target value is constantly updated and the evolution cycle continues until the termination condition has been met. The termination condition in our implementation is defined as a maximum number of iterations of simulation or final convergence accuracy.
Particle Swarm Optimization (PSO).
The PSO is a population based stochastic optimization method which was proposed by Eberhart and Kennedy in 1995. It simulates the swarm behavior which looks for food in a cooperative way of insects, herds, birds and fish. For example, when a group of birds are looking for food, each bird inside will be abstracted into a particle with position and speed and each particle will change its possible future activity trend and trajectory according to its own personal experience as well as the experience of other members. Similarly to the GA, the PSO has been used for parameter calibration in some hydrological model. The algorithm is initialized to a group of random particles, that is random solutions and then the optimal solution is obtained iteratively. At every step of the iteration, the velocity of each particle is updated according to the current individual best position found by itself and the current global best position shared by the whole particle swarm. If the swarm consists of N particles and the maximum iteration counters is max_iter, the velocity and position of a single particle are updated at t iteration by the following formula:
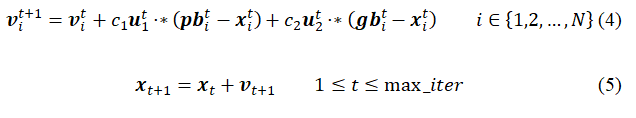
Where vectors v and x are the velocity and the position of the particle separately; pb is the best position previously occupied by the particle; gb is the best position previously occupied by any particle of the global swarm; u1 and u2 are vectors of random values between 0 and 1. The velocity and the position of each particle in the global space are updated independently by the above two equations. The flowchart of our parallel PSO is shown in Figure 5.
In our work, the position vector of the particle corresponds to a set of parameters in the water cycle simulation process. We will take a simple model of three sub-basins, of which the first and the second are upstream sub-basins and the last one is the corresponding downstream sub-basin as an example to explain the specific meaning of particle position and velocity in the simulation. The relationship between input x and output y in each sub-basin is defined as:
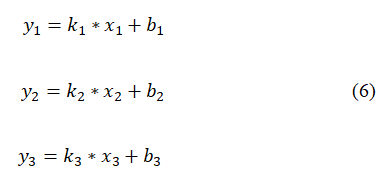
And the vector x which is each particle’s position representing a set of parameters for all sub-basins is defined as:
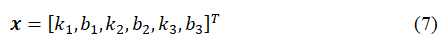
And the v which is each particle’s velocity representing the variation of each parameter is also a vector corresponding to the position, that is,
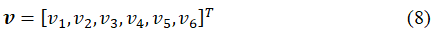
If the component direction of v is positive, it means that every component of the vector x will increase by the corresponding value and if the component direction is negative, it will decrease. As for the best solution, the local optimal solution of each particle refers to the parameter values corresponding to the optimal R2 coefficient that appears for each particle as of the current time step and the global optimal solution corresponds to the optimal coefficient appearing in all particles as of the current time step.
Results and Discussion
In the above sections, we described how to calibrate the parameters in water cycle simulation and find out the optimal set of parameters. Although a set of optimal parameters can be selected through specific algorithms and methods to make the hydrological simulation results closest to the actual situation and achieve the optimal effect, the demand of calculation for parameters of each sub-basin will increase geometrically in large scale simulation, resulting in too long time for real-time applications. We need to meet the calibration requirements in high spatial dimension and long time span in this large scale case, so we developed parallel versions of our GA and PSO. In our parallel implementation, we adopt a master slave implementation and split the domain owned by the MPI processor to make full use of the advantages of multicore CPUs. The optimization space of the whole set of parameters is allocated to each sub domain for calculation and the algorithm is introduced into each sub domain to speed up the iteration. Our approach maintains a good level of cooperation among sub domains, performs parameter iteration in parallel, accelerates parameter calibration and makes full use of computing resources.
In our experiments, we compare the performance of the GA and the PSO using 8192 parameters from Ganjiang sub-basins on TianHe-2 supercomputer. The initial conditions are shown in Table 1. Each sub domain including two processes performs the water cycle simulation based on Wetspa runoff model and Muskingum routing model. We first calibrate the hydrological data for the first half of 2018 and then use this model to simulate for the second half of the year. As previously stated, the fitting accuracy we used is measured by index R2 and the closer the value is to 1, the better the calibration effects.
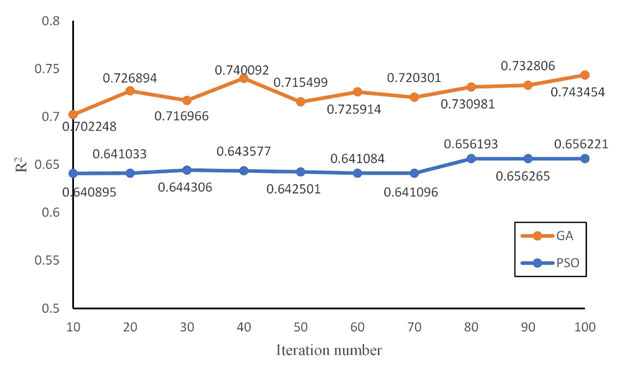
The trend of R2 based on the GA and PSO within 100 iterations during calibration period is shown in Figure 6. It can be seen that the calibration results converge to 0.74 and 0.65 based on GA and PSO, respectively, as the number of iterations increases. The convergence values of the algorithms during simulation period are shown in Table 2, where the final convergence result of GA is higher than that of PSO and consistent with results in calibration period. In addition, fitting accuracy of the calibration results associated with GA exceeded 0.8 to meet the desired expectations after 1000 iterations. It can be concluded that our method works. Moreover, it can be analyzed that the iteration of PSO depends on its own optimal value as well as global optimal value, so it is easy to make parameters fall into local optimal value. Since the GA operates with genetic mutation when performing parameter calibration, it ensures that the population is diverse and therefore looks beyond the global optimum to find a wider range of solutions.
| Parameters | Values |
|---|---|
| Number of iterations | 100,500 and 1000 |
| Calibration accuracy | 0.8 |
| Crossover rate (GA only) | 0.88 |
| Mutation rate (GA only) | 0.1 |
| c1 (PSO only) | 2 |
| c2 (PSO only) | 2 |
Table 1: Algorithm parameter values.
| Number of iterations | Algorithms | |
|---|---|---|
| GA | PSO | |
| 100 | 0.761534 | 0.639657 |
| 500 | 0.791308 | 0.639676 |
| 1000 | 0.831248 | 0.639826 |
Table 2: Comparison of convergence values of GA and PSO.
The speedup and parallel efficiency of our parallel GA and PSO are plotted in Figure 7 and Figure 8. We can find that the speedup of GA and PSO increases as the number of processes increases, but the speedup of the GA slows down at 256 processes, while the PSO still increases at a speedup close to the ideal. As the parameter update of the GA is more complex, the master process takes up the core work, such as parameter selection, crossover and mutation, while the slave processes are mainly responsible for the calculation of the water cycle simulation, so the computation of the master process cannot be effectively reduced in the process of adding slave processes. In contrast, the parameter update of the PSO is simpler and its speedup increases significantly as the number of processes increases. However, due to the consumption of processes communication, the more the number of processors, the more frequent the communication will be which in turn leads to a decrease in the parallel efficiency of the processor as the number of processes increases.
From the above test results and summary, it can be concluded that the parallel genetic algorithm and the parallel particle swarm algorithm are suitable for different hydrological simulation application due to their respective characteristics; parallel genetic algorithm is used for accurate hydrological models or for long-term simulations and parallel particle swarm algorithm is used for short-term simulations for real-time predictions.
Conclusion
This paper presents a parameters optimization solution for large scale hydrological simulation which considers multiplicity of parameters and the complexity of sub-basins. We used two optimization algorithms, the GA and the PSO, to attack the complexity of high dimensional parameters and produce solutions in a relatively short computation time. The computing time is further reduced through parallelization of optimization algorithms. After obtaining convergence results essentially around 0.65 and the parallel efficiency of 95.9% on 32 cores, we conclude that, it is possible to achieve high dimensional parameters calibration in large scale hydrological simulation by using a parallel implementation on multicore CPUs, that is the optimal parameters can be obtained in a relatively short computation time while ensuring correctness of simulation results. In addition, our comparison of the two algorithms shows that the final result of convergence of the GA is better than the PSO and that the acceleration effect of the PSO is more obvious than the GA. It is necessary to combine the characteristics of the two algorithms in the specific use of parameters.
References
- Huong HTL, Pathirana A (2013) Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol Earth Syst Sci 17:379-394.
- Kratzert F, Klotz D, Brenner C, Schulz K, Herrnegger M (2018) Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol Earth Syst Sci 22:6005-6022.
- Zhang L, Yang X (2018) Applying a multi-model ensemble method for long-term runoff prediction under climate change scenarios for the yellow river Basin, China. Water 10:301.
- Yazdi NM, Ketabchy M, Sample DJ, Scott D, Liao H (2019) An evaluation of HSPF and SWMM for simulating streamflow regimes in an urban watershed. Environ Model Softw 118, 211-225.
- Yu Z (2015) Hydrology, floods and droughts modeling and prediction. Encycl Atmos Sci 217-223.
[Crossref]
- Brezinski C (2000) Acceleration procedures for matrix iterative methods. Numer Algorithms 25:63-73.
- Fread DL, Harbaugh TE (1971) Open-channel profiles by Newton’s iteration technique. J Hydrol 13:70-80.
- Boyle DP, Gupta HV, Sorooshian S (2000) Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods. Water Resour Res 36:3663-3674.
- White LW, Vieux B, Armand D, LeDimet FX (2003) Estimation of optimal parameters for a surface hydrology model. Adv Water Resour 26:337-348.
- Seibert J (2000) Multi-criteria calibration of a conceptual runoff model using a genetic algorithm. Hydrol Earth Syst Sci 4:215-224.
- Gill MK, Kaheil YH, Khalil A, McKee M, Bastidas L (2006) Multiobjective particle swarm optimization for parameter estimation in hydrology. Water Resour Res 42.
- Vrugt JA, Gupta HV, Bouten W, Sorooshian S (2003) A shuffled complex evolution metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour Res 39.
- Feng Z, Niu W (2021) Hybrid artificial neural network and cooperation search algorithm for nonlinear river flow time series forecasting in humid and semi-humid regions. Knowl Based Syst 211:106580.
- Efstratiadis A, Koutsoyiannis D (2010) One decade of multi-objective calibration approaches in hydrological modelling: A review. Hydrol Sci J 55:58-78.
- Kollet SJ, Maxwell RM, Woodward CS, Smith S, Vanderborght J, et al. (2010) Proof of concept of regional scale hydrologic simulations at hydrologic resolution utilizing massively parallel computer resources. Water Resour Res 46.
- Li T, Wang G, Chen J, Wang H (2011) Dynamic parallelization of hydrological model simulations. Environ Model Softw 26:1736-1746.
- Li Y, Jiang DL (2014) Dynamic task-scheduling based parallel processing on watershed distributed eco-hydrological model. Appl Mech Mater. 556-562:3492-3495.
- Xu D, Wang W, Chau K, Cheng C, Chen S (2012) Comparison of three global optimization algorithms for calibration of the Xinanjiang model parameters. J Hydroinform 15:174-193.
- Duan Q, Sorooshian S, Gupta V (1992) Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour Res 28:1015-1031.
- Duan Q, Sorooshian S, Gupta VK (1994) Optimal use of the SCE-UA global optimization method for calibrating watershed models. J Hydrol 158:265-284.
- Bakhtyar R, Barry DA (2009) Optimization of cascade stilling basins using GA and PSO approaches. J Hydroinform 11:119-132.
- Wang QJ (1991) The genetic algorithm and its application to calibrating conceptual rainfall-runoff models. Water Resour Res 27:2467-2471.
- Qin Y, Kavetski D, Kuczera G (2018) A Robust Gauss‐Newton algorithm for the optimization of hydrological models: From standard Gauss‐Newton to robust Gauss‐Newton. Water Resour Res 54:9655-9683.
- Zhang X, Srinivasan R, Zhao K, Liew MV (2009) Evaluation of global optimization algorithms for parameter calibration of a computationally intensive hydrologic model. Hydrol Process 23:430-441.
- Fazal MA, Imaizumi M, Ishida S, Kawachi T, Tsuchihara T (2005) Estimating groundwater recharge using the SMAR conceptual model calibrated by genetic algorithm. J Hydrol 303:56-78.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi