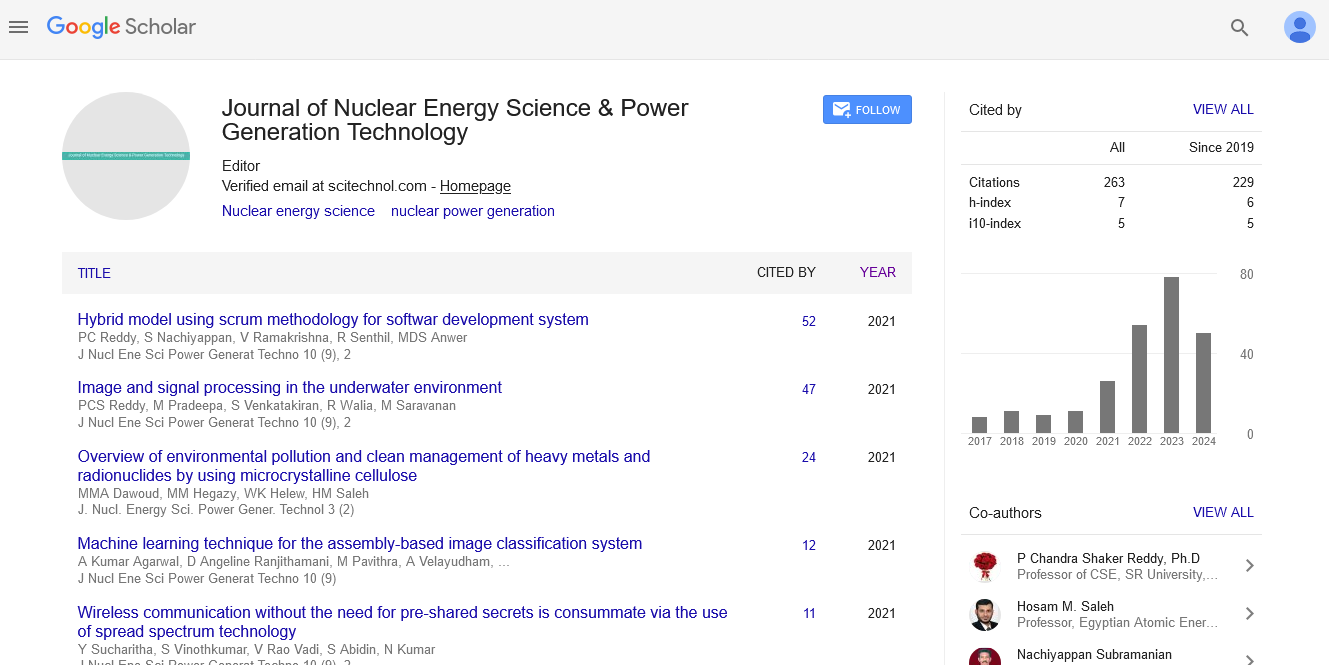
Research Article, J Nucl Ene Sci Power Generat Technol Vol: 10 Issue: 4
Compact Tree Structures for Mining High Utility Itemsets
Hailye Tekleselase*
Department of Information Systems, Wolaita Sodo University, Addis Ababa, Ethiopia
*Corresponding author:
Tekleselase H, Department of Information Systems, Wolaita Sodo University, Addis Ababa, Ethiopia
E-mail: hailyie83@gmail.com
Received date: September 29, 2021; Accepted date: October 13, 2021; Published date: October 20, 2021
Citation: Haliye T (2021) Compact Tree Structures for Mining High Utility Itemsets. J Nucl Ene Sci Power Generat Technol 10:11.
Abstract
High Utility Itemset Mining (HUIM) from large transaction databases has garnered significant attention as it accounts for the revenue of the items purchased in a transaction. While most tree-based algorithms to mine HUIs transform the database to an item-prefix tree, they discard the unpromising items and consume a significant amount of memory. Employing trees that store transaction-level information has proven to enhance the mining process in conjunction with such prefix trees. In this regard, the present work proposes memory-efficient trees namely- Utility Prime Tree (UPT), Prime Cantor Function Tree (PCFT), and String based Utility Prime Tree (SUPT) that encode entire transaction information in a node, unlike the prefix-based trees through a single database scan. Experiments conducted on both the real and synthetic datasets show that these structures consume significantly less memory when compared to the tree structures in the literature.
Keywords: High Utility Itemset Mining, Tree based algorithms
Introduction
Mining frequent itemsets from a large transaction database is an indispensable step in obtaining patterns that indicate associations among items. Such a task addresses the market basket analysis problem of identifying frequently purchased items by a customer on his visit to a supermarket store. Since its inception, Frequent Itemset Mining (FIM) has been applied in diverse areas such as Text Mining, Bioinformatics, and Pharmacovigilance and so on and has delivered novel insights. Amongst plethora of application areas recommendation systems, Intrusion Detection Systems, Web-click analysis are noteworthy. Due to its versatility, FIM is viewed as a general and popular data mining task.
FIM algorithms are designed to consider only the frequency of occurrence of an itemset in a transaction database. However, the factors such as purchase quantities of items and their unit profit are not handled. Consequently, the patterns obtained are devoid of the revenue information. High Utility Itemset Mining (HUIM) provides for a model where the aforementioned factors can be accommodated during mining. Hence, this area has played a pivotal role since the past decade as a more generalised form of FIM. Most of the algorithms employed for FIM work on the downward closure property of the support or frequency of an itemset in order to enumerate the patterns. However, the revenue or utility measured as unit Prof it purchase quantities is neither monotone nor ant monotone. E.g., if the database shown in considered, the utilities of itemsets are respectively. If the user defined threshold of minimum utility to extract the high utility patterns were set to 18, then the high utility itemset contains both a high utility and low utility subsets [1]. Hence, the utility measure for an itemset does not satisfy the downward closure property.
Materials and Methods
The utility measure carries a broader significance that may vary depending on the domain where these algorithms are applied, and the intent of the study. E.g., certain studies have incorporated correlation of items, discount or cost variations of items in conjunction with the utility. Additionally, HUIM algorithms have been applied in different fields such as mobile commerce, web mining, and biomedicine facilitating efficacious applications.
HUIM has evolved from two-phase to single phase algorithms. Although there is an absence of downward closure property, studies have explored various measures to prune the search space and efficiently mine High Utility Itemsets (HUIs). Generally, the algorithms discard the items that are deemed to be unpromising during the initial phase when a data structure such as a tree or a list is constructed. If a user requests for mining with a lower threshold, certain unpromising items may turn out to be promising mediating data structure reconstruction from scratch. Also, varying the threshold is a plausible scenario amongst decision makers. The patterns obtained at different thresholds get adjudged by the decision makers for interestingness before arriving at a consensus. Primarily, the thresholds and interestingness measures are varied to suite the intended application of the mining task. Apart from this, quality decision making requires the algorithm to ensure better inter activeness instead of repeated data structure construction prior to mining. Apart from this, the trees occupy significant amount of memory as the transaction databases are voluminous and mostly sparse. Further, the divide and conquer strategy employed during the mining phase is a recursive process that necessitates the creation of large number of conditional pattern trees. This can overwhelm the memory space and hence adversely affect the mining performance.
Recently, an algorithm called SPUC was proposed. In this study, the authors proposed two tree structures-a transaction-level compressed tree called SUT (String Utility Tree) along with a conventional prefix tree called Utility Count Tree (UCT) for mining HUIs in a single-phase. In order to alleviate the aforementioned shortcomings, the current work proposes and evaluates trees similar to SUT that compactly represent the transaction database. Most of the existing trees encode the database information on a per item basis for each transaction. In contrast to this, the proposed tree structures compactly represent the information in the nodes of the tree at the transaction level thus providing a higher abstraction. Also, the memory efficiency of these structures namely Utility Prime Tree (UPT), Prime Cantor Function Tree (PCFT), and String based Utility Prime Tree (SUPT) have been compared with the Utility Count Tree (UCT). The significance and advantages of the proposed tree structures are enumerated below:
- All these trees are complete i.e., these are constructed using a single database scan without discarding any items. This ensures faster construction as multiple database scans (a costly I/O operation) in discarding the unpromising items is overcome.
- The trees are compact due to the encoding of information with respect to a transaction rather than per item basis in the nodes of the trees. Also, experimental evaluations prove that they are memory efficient
The rest of this paper is organized as follows. In subsections 2.1 and 2.2 of Section 2 formal concepts and related work in the area of HUIM have been described. The proposed data structures have been detailed in Section 3. The paper concludes with experimental evaluation and conclusion provided in Section 4 and 5 respectively (Table 1).
| Item | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Profit | 5 | 2 | 1 | 2 | 3 | 5 | 1 |
| (b) Transaction Table | |||||||
| TID | Transaction | ||||||
| T1 | {(3,1)(5,1)(1,1)(2,5)(4,3)(6,1)} | ||||||
| T2 | {(3,3)(5,1)(2,4)(4,3)} | ||||||
| T3 | {(3,1)(1,1)(4,1)} | ||||||
| T4 | {(3,6)(5,2)(1,2)(7,5)} | ||||||
| T5 | {(3,2)(5,1)(2,2)(7,2)} | ||||||
Table 1: Sample database.
Background
Preliminary:Given a transaction database D, each transaction Td in D is identified by TID, the transaction identifier and records a collection of items purchased along with its quantity or internal utility. Formally, T I where I = fi1; i2; i3; ing denotes the collection of items. A typical transaction database. An ordered pair (ix; qx) in each transaction indicates that the item ix was purchased in qx quantities in that transaction. Each item is also associated with unit profit or external utility as shown.
Related Work
For an itemset X, the TWU is an upper bound on the utility, u(X) and antimonotone. Hence, most of the algorithms that generate and test candidates in a level-wise manner employ this measure to prune the search space [2]. However, such a level-wise approach is time consuming owing to the repeated database scans to determine the TWU of large number of candidate itemsets. Further, the join operation adds to the complexity of enumerating higher order itemsets. In order to alleviate this problem, several algorithms have been proposed that transform the information in the database to a data structure. The subsequent mining involves operating on this data structure without the necessity of scanning the database.
In this regard, the role of HUP-Growth, HUC-Prune based on FP- Growth is significant. While both the algorithms transform the database into a tree with a node for every item of a transaction, the former captures the quantity information in one of the elements of the node. Due to the absence of a mechanism to enumerate itemsets from the HUP-tree efficiently, a lot of candidate itemsets are generated. In contrast, HUC-Tree employs the TWU Downward Closure Property and employs pattern growth approach to enumerate candidate HUIs. Although both the algorithms generate significantly lesser number of candidates in comparison to the Two-Phase algorithm, the tree structure needs to be reconstructed once the user defined threshold for minimum utility, i.e., minutil is modified.
UP-Growth and UP-Growth+are the efficient state of the art tree based algorithms. Here, the authors proposed several strategies to prune the search space during construction and recursive mining of the UP-Tree. At the very outset, during the first database scan, those 1-items that were not HTWUI are discarded. Further, the utilities of each item is calculated without considering its descendants. In a similar manner, during the mining operation local UP-trees are constructed after discarding local unpromising items and decreasing minimum utilities of descendant nodes. The bounds are further strengthened in UP-Growth+ based on path utilities and estimated utilities of descendant nodes.
Compact tree structures for mining high utility itemsets
In order to facilitate efficient incremental and interactive mining of HUIs, IHUP algorithm that constructs tree without ignoring any items based on TWU was proposed. Authors proposed three different approaches of tree construction-based on lexicographic order of items called IHUPL-Tree, based on descending order of Transaction Frequency called IHUPTF-Tree and based on descending order of TWU called IHUPTWU-tree. After every N transaction is read, IHUPTF-Tree and IHUPTWU-tree has to be reordered that increases the data structure construction time.
Apart from the tree based algorithms, several list based algorithms are available in the literature such as HUI-Miner, HUP-Miner, d2HUP. These algorithms are mostly single-phase and employ pruning strategies for efficient mining. However, the memory consumed in storing the Utility Lists and the costly comparison and join operation is a severe performance bottleneck [3]. Further, recent studies have indicated that trees can outperform list based and projection based algorithms. In addition to this, recently a single-phase trees based algorithm called SPUC (Single-phase Utility Computation) was proposed. In SPUC mining process was guided by a conventional prefix tree called UCT and converged in a single-phase with exact utility information stored in transaction level compressed String Utility Tree (SUT). The authors demonstrated the efficiency of SPUC algorithm in comparison to IHUP, UP-Growth, and UP-Growth+ algorithms. Thus, the current study aims to compactly represent the transaction information in a tree so as to ensure completeness and memory efficiency.
In this section three different tree structures are proposed to represent the transaction database namely:
- Utility Prime Tree (UPT)
- Prime Cantor Function Tree (PCFT)
- String based Utility Prime Tree (SUPT)
The following subsections are dedicated to each of these tree structures where the node structure and brief procedure of representing the information in the database is described. Although UCT is first proposed in it has been briefly described here for the benefit of the readers.
Utility count tree
A node in the Utility Count Tree has the following fields:
- item that denotes the name of the item,
- count that indicates the count of the item in the given path of the tree,
- utility that accumulates the utility of the item in the given path of the tree,
- parent pointer that points to the parent of the node
UCT is constructed without discarding any items during the initial tree construction unlike HUP-Growth or HUC-Prune. The database is scanned and a node N is constructed for every item in a transaction Tj. The brief procedure for inserting transactions into UCT is provided in Algorithm. Initially N is set to the root node of the tree. The items in the transaction are inserted as child nodes of one another. Hence, each path of the tree corresponds to a particular transaction. If a transaction contains a node that is already present in the tree, the procedure updates the count and utility instead of creating a new node in the given path. This ensures prefix sharing. The UCT for sample database displayed in (Figure 1).
Database with a single scan of the database, UCT captures relevant information in its tree structure. Although the count field indicates the number of transactions a given item is participating, reconstructing the database from this information is not possible. For example, consider the paths < 3; 5; 2; 4 > and < 3; 5; 2; 7 > for UCT. The count field for item 2 has the value 2 as it is participating in two transactions, T2 and T5. However, the utility value is cumulative of utilities in these two transactions and does not enable in resolving the utility individually across the two transactions (Figure 2).
Utility prime tree
Utility Prime Tree captures the transaction level information in a single node unlike the UCT. The items and utilities are mapped to corresponding prime numbers by employing them as indices. The assigned prime numbers are then stored compactly in a node of the UPT. Every node of the UPT contains the following fields:
- primeItems This field stores the product obtained after multiplying the prime numbers assigned to every item of a transaction
- T U This field stores the Transaction Utility of a transaction
- primeU tility(Tj) This field stores the product obtained after multiplying the prime numbers assigned to utility of every item of a transaction
- parent pointer that points to the parent of the node.
UPT compactly stores the database information by capturing the information at the transaction level instead of creating node for every item in a transaction. However, as the number of items and transactions increase, the space required to store the product, primeU tility(Tj) overwhelms the allocated node space. Hence, factorising and subsequent resolution of utilities of items is not facilitated.
Brief procedure to construct PCFT is provided in Algorithm. Displays the PCFT although the tree is complete and ensure database reconstruction, the main drawback is absence of path sharing as evident. For example, while T2 and T3 appear as child of T1 in UPT as items(T2) items(T1) and items(T3) items(T1), due to the uniqueness in mapping of (ix; u(ix; Tj)) through CF prior to prime encoding, the sharing is absent in PCFT. With PCFT, if items are purchased in similar quantities across two transactions Ti and Tj such that either items (Ti) items (Tj) or items (Tj) items (Ti) sharing can be ensured.
Utility values are used along with items in the cantor function prior to assigning them with the corresponding prime numbers. If an item is present in two different transactions, CF maps the item-utility pair to a unique number and hence the same item may get assigned to different prime numbers if the utility values are different. This limits the prefix sharing in the PCFT owing to the inherent feature of the CF. The major implementation drawback is due to the large value obtained to store primeCF (Tj) for every transaction. This is bound to increase overwhelmingly with growing number of items in the database (Figure 3).
String based utility prime tree
This tree is similar to UPT. In order to overcome the problem of storing large number that arises from computing primeItem (Tj), the prime numbers assigned to items and utilities are concatenated by a delimiter. As this information is stored in textual format, substring comparison is performed while inserting transactions into the tree structure to identify the transactions containing common set of items. This ensures prefix-sharing. Also, it is possible to reconstruct the entire database due to the string representation of the primeItems and primeU tility. The procedure and SUPT for sample database is displayed in Algorithm 4 respectively (Figure 4 and Table 2).
| Dataset | jDj | jIj | T | Density(%) |
|---|---|---|---|---|
| Chess | 3196 | 75 | 37 | 49.33 |
| Mushroom | 8124 | 119 | 23 | 19.32 |
| Foodmart | 4141 | 1559 | 4.4 | 0.28 |
| Retail | 88162 | 16470 | 10.3 | 0.06 |
| Connect | 67557 | 129 | 43 | 33.33 |
Table 2: Characteristics of real datasets.
SUPT bears slight resemblance to the String Utility Tree proposed. While SUT directly concatenates the items and utilities using a delimiter, SUPT resorts to prime encoding prior to concatenation.
Experimental evaluation
The source code implementation in Java provided by SPMF was extensively used to implement the algorithms of the proposed tree structures. Experiments were conducted on both real and synthetic datasets to compare the execution time and memory consumed by the proposed tree structures against the two popular tree structures in the literature namely, IHUP and UP-Growth trees. Table 2 records the characteristics of the datasets used. For the experiments, a system with 8GB RAM, Windows 7 OS with Intel Core i5 processor at 3.00 GHz was used (Figure 5).
Performance analysis on real datasets
Depicts the execution time of the algorithms. Across all the datasets, UCT executed faster than the remaining algorithms. The percentage improvement obtained due to UCT in comparison to IHUP and UP-Growth trees is recorded in Table 3. Among the prime-based trees, UPT performed better, especially when the dense datasets were considered. As shown in the figure, it executed faster than UP-Growth by 66%, 36% and 65% on Chess, M ushroom and Connect datasets respectively. Also, PCFT performed 48:8% faster than UP-Growth on Connect dataset. However, its performance was poor on large and sparse datasets such as, F oodmart and Retail. Owing to the longer execution time, PCFT was executed on only 100 and 500 transactions of these two datasets. The larger values obtained after applying CF to (ix; u(ix; Tj)) pair increased the prime encoding time that subsequently affected the overall execution time. Although SUPT took longer time for construction, it performed significantly faster on F oodmart, one of the sparse datasets where PCFT failed [4]. The low value of T for this dataset ensured the presence of common set of items across different transactions leading to lesser string comparisons during the tree construction.
Denotes the memory consumed by the proposed structures in comparison with IHUP and UP-Growth trees. The getObjectSize (Object) method of Instrumentation interface implemented and provided in sizeof package was used to calculate the amount of memory consumed. Due to longer execution time only 100 and 500 transactions of F oodmart and Retail was considered. The prime-based tree structures clearly consumed significantly lesser space in comparison to the remaining trees. The transaction level encoding of database information ascertains the lower memory (Table 3 and Figure 6).
| Dataset | IHUP | UP-Growth |
|---|---|---|
| Chess | 76.47 | 91.56 |
| Mushroom | 64.26 | 91.38 |
| Foodmart | 72.1 | 92.91 |
| Retail | 64.76 | 99.82 |
| Connect | 50.83 | 99.48 |
Table 3: Percentage improvement in execution time of UCT in comparison to IHUP and UP-Growth trees.
On an average across Chess dataset, UPT, PCFT, and SUPT consume 19:5, 19:5 and times lesser memory than IHUP and UP-Growth trees. Across M ushroom, in the same order the reduction in memory was 5.2, 5.2 and 5.8 times. Due to partial database considered when running PCFT implementation of F oodmart, UPT and SUPT consumed 5.9 and 6.5 times lesser space. This reduction for the two trees was about 12.6 and 13.3 in the case of Retail, another sparse dataset. A reduction of about 8.6 and 9.7 times was observed when Connect dataset was considered. Although PCFT has only two fields, the prefix sharing is easier across SUPT than in PCFT. Hence SUPT turned out to be memory efficient among the proposed trees (Tables 4 and 5).
| Dataset | UPT | PCFT | SUPT |
|---|---|---|---|
| Chess | 19.97 | 19.97 | 22.57 |
| Mushroom | 5.21 | 5.21 | 5.89 |
| Foodmart | 5.95 | 255.4 | 6.56 |
| Retail | 12.64 | 2226.04 | 13.31 |
| Connect | 8.61 | 57.01 | 9.75 |
Table 4: Space reduction in comparison to IHUP.
| Dataset |
UPT |
PCFT |
SUPT |
|---|---|---|---|
Chess |
19.16 |
19.16 |
21.66 |
Mushroom |
5.2 |
5.2 |
5.89 |
Foodmart |
5.91 |
253.54 |
6.51 |
Retail |
12.64 |
2226.04 |
13.31 |
Connect |
8.61 |
57.01 |
9.75 |
Table 5: Space reduction in comparison to UP-Growth.
Performance analysis on synthetic datasets
In order to further evaluate the performance of the proposed structures, synthetic datasets were generated using the SPMF tool. First set of datasets were mostly dense and their characteristics are provided in Table 6 where the parameter Tmax denotes the maximum transaction length (Table 6).
| Dataset | jDj | jIj | Tmax | Density(%) |
|---|---|---|---|---|
| d01 | 5000 | 100 | 10 | 5.54 |
| d02 | 5000 | 100 | 50 | 25.53 |
| d03 | 5000 | 500 | 10 | 1.09 |
| d04 | 5000 | 500 | 50 | 5.04 |
| d05 | 10000 | 100 | 10 | 5.43 |
| d06 | 10000 | 100 | 50 | 25.61 |
| d07 | 10000 | 500 | 10 | 1.1 |
| d08 | 10000 | 500 | 50 | 5.1 |
Table 6: Characteristics of synthetic dense datasets.
The execution time of different algorithms is compared. As in the case of real datasets, UCT clearly outperformed all the algorithms. Records the percentage improvement obtained in execution time when UCT was compared with IHUP and UP-Growth trees. On an average an improvement of 82:82% on IHUP and 52:49% on UP-Growth was observed. Among the prime-based trees, UPT and SUPT showed promising results. Further, on very dense datasets like d02 and d06, PCFT executed faster than SUPT, although not considerably. However, as the datasets became relatively sparse its performance degraded, especially in the case of d03 and d07 where SUPT and UPT (Figure 7).
Performed significantly better this indicates that PCFT is more sensitive to sparseness. In the case of UPT and SUPT the increase in execution time with the increase in density for a constant database size was significant in contrast to PCFT. Especially in the case of d03 and d04 where the change in density was around 4 units, execution time of PCFT was almost the same while there was sharp increase in execution time of both UPT and SUPT. This indicates that UPT and SUPT are more sensitive to density changes for a given size of the database than PCFT (Table 7 and Figure 8).
| Dataset | UP-Growth | IHUP |
|---|---|---|
| d01 | 83.24 | 44.24 |
| d02 | 89.83 | 78.16 |
| d03 | 81.96 | 45.45 |
| d04 | 85.59 | 66.09 |
| d05 | 80.34 | 32.74 |
| d06 | 84.42 | 58.65 |
| d07 | 74.08 | 44.48 |
| d08 | 83.14 | 64.53 |
Table 7: Percentage improvement in execution time of UCT across synthetic dense datasets.
Further, the memory consumed by the various structures was compared as shown in Figure 8. SUPT turned out to be the memory efficient one. For a given database size, although the memory taken up by tree structures seemed to be mostly independent of the changing density, SUPT showed slight variations when compared to other prime-based trees. This difference was evident with growing database size. Record the factor-wise memory consumption of Prime Trees in comparison to IHUP and UP-Growth trees. Comparison on real and synthetic dense datasets indicated that UCT is more time efficient whereas SUPT is more memory efficient (Table 8 and 9).
| Dataset | UPT | PCFT | SUPT |
|---|---|---|---|
| d01 | 5.89 | 5.9 | 5.92 |
| d02 | 37.5 | 37.78 | 40.82 |
| d03 | 7.08 | 7.01 | 7.24 |
| d04 | 39.95 | 40.44 | 43.72 |
| d05 | 5.56 | 0.562 | 5.55 |
| d06 | 37.77 | 37.06 | 40.11 |
| d07 | 6.95 | 6.77 | 6.89 |
| d08 | 39.94 | 40.35 | 44.99 |
Table 8: Space reduction in comparison to IHUP.
| Dataset | UPT | PCFT | SUPT |
|---|---|---|---|
| d01 | 5.89 | 5.9 | 5.92 |
| d02 | 37.5 | 37.78 | 40.82 |
| d03 | 7.08 | 7.01 | 7.24 |
| d04 | 39.95 | 40.44 | 43.72 |
| d05 | 5.56 | 0.562 | 5.55 |
| d06 | 37.77 | 37.06 | 40.11 |
| d07 | 6.95 | 6.77 | 6.89 |
| d08 | 39.94 | 40.35 | 44.99 |
Table 9: Space reduction in comparison to UP-Growth.
In order to further explore the characteristics, experiments were conducted to compare these two structures on sparse datasets. The characteristic of the datasets is described in depict the execution time and space consumed respectively. UCT performed graciously even with sparsest of the datasets. However, SUPT clearly outperformed UCT in terms of memory requirements (Table 10 and Figures 9 and 10).
| Dataset | jDj | jIj | Tmax | Density(%) |
|---|---|---|---|---|
| s01 | 10000 | 10000 | 10 | 0.055 |
| s02 | 10000 | 10000 | 50 | 0.257 |
| s03 | 10000 | 50000 | 10 | 0.017 |
| s04 | 10000 | 50000 | 50 | 0.051 |
| s05 | 100000 | 10000 | 10 | 0.055 |
| s06 | 100000 | 10000 | 50 | 0.255 |
| s07 | 100000 | 50000 | 10 | 0.011 |
| s08 | 100000 | 50000 | 50 | 0.051 |
Table 10: Characteristics of synthetic sparse datasets.
Inferences
In the previous section, the proposed tree structures were compared with IHUP and UP-Growth which are item-based prefix trees. As IHUP involves reordering the tree after N transactions and UP-Growth involves two database scans for complete tree construction, such overheads were eliminated in UCT leading to faster execution. In terms of memory requirements, the prime trees were more efficient due to the transaction level encoding of information [5]. Among these, SUPT was more efficient across real and synthetic datasets owing to better prefix-sharing. As the datasets became sparser, PCFT performed poorly in terms of execution time. However, for database of shorter transactions, PCFT can be selected as it displayed faster execution. Overall, UCT and SUPT are promising choices for tree constructions.
Conclusion
With ever increasing database sizes the need for accommodating the essential utility information from is of prime importance. In this regard, the current work proposes tree structures that are constructed via a single database scan without neglecting any items. Especially the proposed prime-based tree structures namely, Utility Prime Tree, Prime Cantor Function Tree and String based Prime Utility Tree have been promising ways of storing the database information in a compact manner in the memory. Apart from this, it was demonstrated that Utility Count Tree is not only time efficient on real datasets but also on large sparse and dense databases. This work can be extended further to mine high utility itemsets from very large databases in a distributed environment.
References
- Burnett K, Ng KB, Park S0020(1999) A comparison of the two traditions ofmetadata development. JASIST 50:1209-1217.
- Mishra P, Jimmy L, Ogunmola GA, Phu TV, Jayanthiladevi A, et al (2020)Hydroponics cultivation using real time iot measurement system. J Phys Conf 12: 012-040.
- Ding Y, Foo S (2002) Ontology research and development. Part I - A review ofontology generation. J Inf Sci. 28: 123-136.
- Davenport T, DeLong D, Beers M (1998) Successful knowledge management MIT Sloan Manag Rev. 39: 43-57.
- Deepthi T, Balamurugan K, Uthayakumar M (2021) Simulation andexperimental analysis on cast metal runs behaviour rate at different gatingmodels. Int J Eng Syst Model Simul. 12: 156-64.
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi