Review Article, J Nucl Ene Sci Power Generat Technol Vol: 10 Issue: 9
Analytical Study on Artificial Neural Network Learning Algorithms and Technique
Jeevitha Maruthachalam*
Department of Computer Science and Engineering, United Institute of Technology, Coimbatore, India
*Corresponding Author: Jeevitha Maruthachalam, Department of Computer Science and Engineering, United Institute of Technology, Coimbatore, India, Email: jeevithamaruthachalam92@gmail.com
Received date: 26-May-2022, Manuscript No. JNPGT-22-65040; Editor assigned date: 31-May-2022, PreQC No. JNPGT-22-65040 (PQ); Reviewed date: 14 Jun-2022, QC No. JNPGT-22-65040; Revised date: 30-Nov-2022, Manuscript No. JNPGT-22-65040 (R);Published date: 28-Dec-2022, DOI: 10.4172/23259809.1000308
Citation: Maruthachalam J (2022) Analytical Study on Artificial Neural Network Learning Algorithms and Technique. J Nucl Ene Sci Power Generat Technol 10:9
Abstract
The artificial neural networks are widely used to support the human decision capabilities, avoiding inconsistency in practice and errors based on lack of experience. In this paper we have explored various learning rules in artificial neural networks like preceptron learning, error correction, hebbian and competition learning rules are explored. Learning rules are algorithms which direct changes in the weights of the connections in a network.
They are incorporating an error reduction procedure by employing the difference between the desired output and an actual output to change its weights during training. The learning rule is typically applied repeatedly to the same set of training inputs across a large number of epochs with error gradually reduced across epochs as the weights are fine-tuned. This paper also focuses on one of the neural network technique called Multilayer Perceptron (MLP) along with its applications and advantages and drawbacks.
Keywords: Artificial neural networks; Perceptron learning;
Error correction; Memory based; Hebbian; Competition
learning; MLP
Keywords
Artificial neural networks; Perceptron learning; Error correction; Memory based; Hebbian; Competition learning; MLP
Introduction
An Artificial Neural Network (ANN) is an information processing model which is stimulated by the way our brain process certain information. It is made up of a huge amount of well interconnected processing elements namely neurons. ANNs is similar to human being in terms of learning by example. An ANN is generally configured for a application like pattern recognition or data classification which is achieved through a learning process. Learning in involves repeated change or adjustments to the synaptic associations among the neurons [1].
The problem solving approach of neural networks is completely way apart from the conventional algorithmic approach i.e. the computer follows a set of instructions in order to solve a problem. Computer cannot solve the problem unless and untill the instructions are clear. So the problem solving capability of conventional is that we already understand and know way of solving. But it would be too good if computers could solve problems which don't precisely know how to do. Neural networks process information in way similar to what human brain does [2,3]. Neural networks learn by example. It cannot be programmed to do a particular task. The drawback is that its process is unpredictable since the network finds out how to solve the problem by itself. Conventional systems are predictable, if anything goes wrong it will be because of software or hardware fault [4].
Neural networks and conventional algorithmic computers balance each other. Certain tasks are best suited to an algorithmic approach like arithmetic operations and there are tasks more suited to neural networks and there are number tasks which require sandwich approach (conventional+neural) to achieve with higher effectiveness. Above all it learns from the experiences collected all the way through the earlier training patterns [5].
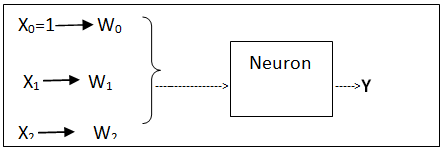
The fundamental of neuron representation is often known as node or unit. Input could be from some other units, or even from an external source. Every input has its weight w, where w can be adjusted to model synaptic learning. The unit computes function f of the weighted sum of its inputs [6,7]. Its output, in turn, could be input to other units. The final weighted sum of inputs is called the net input to unit i, often written neti. Weight from unit j to unit i is denoted as wij. The function f is the unit's activation function. In the simplest case, f is the identity function, and the unit's output is just its net input. This is called a linear unit (Figure 1).
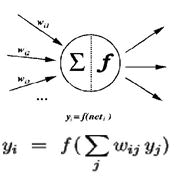
Figure 1: Simple artificial neuron model.
Literature Review
Different learning algorithms
Error-correction learning algorithm: In this, the desired output value will be set and the actual output value is compared with the expected output value. The difference in turn is used to direct the training. The difference is termed as local error and the error values are used to adjust the respective weights through algorithm like back propagation algorithm. Consider the actual output as y, and the desired output as d, the error can be defined as:
e=d-y
With each training iteration the error signal is minimized to a reasonable level. In general back propagation algorithm is used with error-correction learning.
Gradient Descent (GD): The gradient descent algorithm is one of the most powerful ANN learning algorithms. It is widely applied in various fields of science, engineering, and mathematics. The GDA minimizes an error function g(y), through the manipulation of a weight vector w. The cost function can be denoted as below:
Which is the linear combination of the weight vector and an input vector x
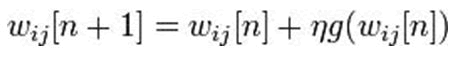
Perceptron algorithm: Perceptron algorithm is one of the oldest and finest algorithms in Artificial Neural Networks (ANN).
It is a network in which the neuron unit calculates the linear combination of its real-valued or boolean inputs and passes it through a threshold activation function, which in case of two input variables is:
Threshold (s)=1 if s >0 and 0 otherwise
There are chances for the systems output to vary from the desired output.
error=d-e
where, d is desired output, e is actual output.
In such cases the weights are adjusted where the activation function could be defined as follows:
Wnew=wold+((error) × xi))
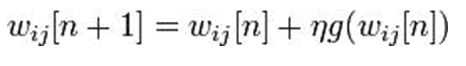
Figure 2: Perceptron learning rule.
Our single-layer Perceptron in this two-dimensional case looks like the following box where the inputs are multiplied by the weights when they enter the function.

Figure 3: Inputs are multiplied by the weights.
Hebbian learning: Hebbian theory is a extremely useful theory in understanding how the neurons in the brain adapt or change during the learning process. The general principle goes as follows:
The synaptic efficacy between two neurons will increase if the two neurons are 'simultaneously' active, and it will decrease if not.
According to artificial neural networks, Hebb’s principle is the method of determining how to adjust the weights between model neurons. The weight between two neurons increases if the two neurons activate simultaneously, and reduces if they activate separately.
Hebb’s rule is often generalized Δωi=È xi yi i.e, the change in the ith synaptic weight ωi is equal to a learning rate ɳ times the ith input times the postsynaptic response. The postsynaptic response can be
• Two neurons are 'positively correlated' if the presynaptic neuron fires before the postsynaptic neuron. The weight increase is greatest when this fire time difference is zero or very small. The weight increase gradually decreases as the spike time difference gets larger.
• Two neurons are 'negatively correlated' if the presynaptic neuron fires after the postsynaptic neuron, excepting for a few brief milliseconds around the equal correlation point'. The weight is decreased for negatively correlated spike times.
• The learning rule is the same for both the pyramidal cell and the inhibitory neuron, although this may not be true for real neurons.
Multilayer Perceptron (MLP) network
The greater part of machine learning uses supervised learning. Supervised learning is something in which you have input variables (x) and an output variable (Y) and you use an algorithm to learn the mapping function from the input to the output [8].
Y=f(X)
The goal is to approximate the mapping function so well that when you have new input data (x) that you can predict the output variables (Y) for that data.
The most common neural network model is the Multilayer Perceptron (MLP). This is one of the best neural network algorithm for supervised network where it requires a desired output in order to learn [9]. The goal of this type of network is to create a model that correctly maps the input to the output using historical data. A graphical representation of an MLP is as shown below:
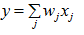
Figure 2: Architecture of MLP.
Discussion
This class of networks consists of multiple layers of computational units, usually interconnected in a feed-forward way. Each neuron in one layer has directed connections to the neurons of the successive layer [10,11]. In many applications the units of these networks apply a sigmoid function as an activation function.
Multi-layer networks use a various learning techniques, among which the well-liked technique is back-propagation. Here, the output values are compared with the correct answer to compute the value of some predefined error-function. By various techniques, the error is then fed back through the network [12]. Using this information, the algorithm adjusts the weights of each connection in order to reduce the value of the error function by some small amount. After repeating this process for a sufficiently large number of training cycles, the network will usually converge to some state where the error of the calculations is small [13]. In this case, one would say that the network has learned a certain target function. To adjust weights properly, one applies a general method for nonlinear optimization that is called gradient descent. For this, the derivative of the error function with respect to the network weights is calculated, and the weights are then changed such that the error decreases. Hence, back-propagation can only be applied on networks with differentiable activation functions [14,15].
Advantages and disadvantages of MLP
Merits of MLP are as follows:
• Connectionist: Can be utilized as a metaphor for biological neural networks.
• Computationally efficient.
• Global computing machines.
• Adaptive learning.
• The capability of learning how to do tasks based on the training data set.
• Best chosen techniques for gesture recognition.
Drawbacks
• Convergence could be time-consuming.
• Local minima can influence the training process.
• Difficult to scale
Applications of MLP
Aerospace: Use in aerospace for
• High performance aircraft
• Flight path simulations
• Aircraft control systems
• Autopilot enhancements
• Automobile automatic guidance systems
• Warranty activity analyzers
Banking:
• Cheque and other document readers
• Credit application evaluators
Defense:
• Weapon steering
• Target tracking
• Facial recognition
• Image signal processing including data compression, feature extraction and noise suppression, signal/image identification
Electronics:
• Code sequence prediction
• Integrated circuit chip layout
• Process control
• Chip failure analysis
• Machine vision
• Voice synthesis
• Nonlinear modeling
Financial:
• Loan advisor
• Mortgage screening
• Credit line use analysis
Manufacturing:
• Manufacturing process control
• Product design and analysis
• Process and machine diagnosis
• Real-time particle identification
Medical:
• Breast cancer cell analysis
• EEG and ECG analysis
• Prosthesis design
• Optimization of transplant
Securities:
• Market analysis
• Automatic bond rating
• Stock trading advisory systems
Conclusion
In this paper, we present the objective of artificial neural network and its applications. In this we explore the error correction, hebbian learning techniques. A detailed study on the Multilayer Perceptron neural network (MLP) is presented. MLP co nstructs global appro-ximations to nonlinear input and output mapping. Consequently they are capable of generalizing in those regions of input where little or no training data is available. Each technique has its own advantages and disadvantages based on the type of neural network architecture and type of training. There is a scope for further research in this area.
References
- Harun N, Woo WL, Dlay SS (2010) Performance of keystroke biometrics authentication system using Artificial Neural Network (ANN) and distance classifier method. Int Conf Comput Commun 1-6.
[Crossref][Googlescholar] [Indexed]
- Schclar A, Rokach L, Abramson A, Elovici Y (2012) User authentication based on representative users. IEEE Trans Syst Man Cybern B Cybern, Part C (Applications and Reviews) 42: 1669-1678.
[Crossref] [Googlescholar] [Indexed]
- Shanmugapriya D, Padmavathi G (2011) An efficient feature selection technique for user authentication using keystroke dynamics. IJCSNS Int J Netw Secur 11: 191-195.
- Maisuria LK, Ong CS, Lai WK (1999) A comparison of artificial neural networks and cluster analysis for typing biometrics authentication. InIJCNN'99. Proc Int Jt Conf Neural Netw. Proceed 5: 3295-3299. IEEE.
[Crossref] [Googlescholar] [Indexed]
- Modi S, Elliott SJ (2006) Keystroke dynamics verification using a spontaneously generated password. Int Carnahan Conference Secur Technol 116-121.
[Crossref] [Googlescholar] [Indexed]
- Peacock A, Ke X, Wilkerson M (2004) Typing patterns: A key to user identification. IEEE Securityand Privacy 2: 40-47.
[Crossref] [Googlescholar] [Indexed]
- Capuano N, Marsella M, Miranda S, Salerno S (1999) User authentication with neural networks. Univerity of Salerno Italy.
- Shorrock S, Yannopoulos A, Dlay SS, Atkinson D (2000) Biometric verification of computer users with probabilistic and cascade forward neural networks. Adv Phys Electron Signal Process Appl 267-272.
- Ross AA, Shah J, Jain AK (2005) Toward reconstructing fingerprints from minutiae points. Biometric Techno Hum Id II 5779: 68-80. SPIE.
- Obaidat MS, Macchairolo DT (1994) A multilayer neural network system for computer access security. IEEE Trans Syst Man Cybern B Cybern 24: 806-813.
- Bleha SA, Obaidat MS (1993) Computer users verification using the perceptron algorithm. IEEE Trans Syst Man Cybern B Cybern 23: 900-902.
[Crossref] [Googlescholar] [Indexed]
- Lin DT (1997) Computer-access authentication with neural network based keystroke identity verification. Proc Int Jt Conf Neural Netw 1: 174-178.
- Jain A, Bolle R, Pankanti S, editors(1999) Biometrics: Personal identification in networked society. Springer Sci Bus Media.
- Kohonen T (1982) Analysis of a simple self-organizing process. Biol cybern 44: 135-140.
[Googlescholar] [Indexed]
- Flanagan JA (1996) Self-organisation in Kohonen's SOM. Neural Netw 9: 1185-1197.
[Crossref] [Googlescholar] [Indexed]
 Spanish
Spanish  Chinese
Chinese  Russian
Russian  German
German  French
French  Japanese
Japanese  Portuguese
Portuguese  Hindi
Hindi