Short Communication, J Phys Res Appl Vol: 8 Issue: 4

A Note on the Solar Neutrino Problem

M. Apostol^*

Department of Theoretical Physics, Institute of Atomic Physics, Magurele- Bucharest Mg-6, POBox MG-35, Romania

*Corresponding Author:

M. Apostol
Department of Theoretical Physics,
Institute of Atomic Physics,
Magurele-Bucharest Mg-6,
POBox MG-35,
Romania;
E-mail: apoma@theory.nipne.ro

Received date: 07 November, 2023, Manuscript No. JPRA-23-119493;
Editor assigned date: 09 November, 2023, PreQC No. JPRA-23-119493 (PQ);
Reviewed date: 22 November, 2023, QC No. JPRA-23-119493;
Revised date: 06 December, 2024, Manuscript No. JPRA-23-119493 (R);
Published date: 13 December, 2024, DOI: 10.4172/jpra.1000122

Citation: Apostol M (2024) A Note on the Solar Neutrino Problem. J Phys Res Appl 8:4.

Abstract

Keywords: Solar neutrinos; Neutrino oscillations; Coupled Dirac equations; Interaction with matter; Admixture angle; Superfluid correlations

Introduction

It is well known that the solar e-neutrinos measured on the Earth are less than the value expected from models of neutrino production in the Sun [1,2]. In order to solve this solar neutrino problem an interaction of the e-neutrinos with matter was suggested [3,4]. It is claimed that such an interaction produces a difference in mass, which would favour the μ-neutrinos [5-9]. However, mass is a Casimir invariant of the Lorentz group which is not affected by interaction. The interaction affects momentum and energy. The coupled Dirac equations of the e- and μ-neutrinos are solved here for a small uniform interaction. It is shown that interaction leads to an increase in the oscillation amplitude of the e-electrons and a decrease of their localization probability. This effect may be related to the solar neutrino problem, though it is much weaker than what would be needed to explain the discrepancy.

Description

Oscillations

We consider two neutrino eigenstates of the free hamiltonian ʋα, α=1, 2, corresponding to admixtures of e- and μ-neutrinos; with usual notations their wave functions (spinors) are

where ΔE=E₂−E₁; we can see the oscillations e ↔ μ. Similar oscillations occur for E₁=E₂ and distinct p’s.

Such neutrinos are produced in the Sun with energies of the order a few MeV ’s; as it is well known, their mass is very small (or even zero). For instance, in the Sun the e-neutrinos interact with electrons; for 1 MeV the neutrino wavelength is ≃ 2 × 10⁻¹¹ cm, which is comparable to the electron Compton wavelength. It follows that the interaction is mainly a forward scattering. The strength of the interaction of a neutrino with an electron is of the order G/Ω, where G ≃ 10⁻⁴⁹erg ·cm³ is the weak-interaction coupling constant and Ω is the volume; it follows that the interaction of an e-neutrino with the medium can be written as

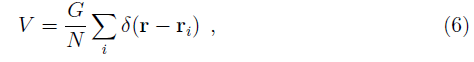
where N is the number of scattering centers, labelled by i; in a first approximation it can be taken as V=Gn ≃ 10⁻²⁴erg (≃ 10⁻¹²eV ), where n is the density of electrons (in the Sun n ≃ 10²⁵cm⁻³). This approximation of a uniform interaction corresponds to neutrinos with relatively moderate energy; for higher energies than the order of localization energy in the nucleus (≃ 10MeV) we may expect anomalies in the interaction effects. Equations (1) and the Dirac equation

Interaction

In the presence of the interaction of the e-neutrinos with matter, these equations become

The probability of localization of the e-neutrinos, interaction included, is

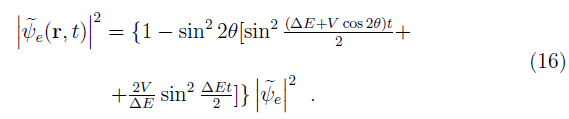
The time average of this probability shows that the interaction leads to an increase of the oscillations amplitude (decrease of the localization probability) by a factor 1+2V/ΔE (ΔE >0). It is worth noting that for ΔE=0 (equal, or vanishing mass) the oscillations are given by 1−sin² 2θ sin²(V t cos 2θ/2). Similar calculations can be done for an admixture of three neutrino flavours, to include the τ-neutrino, with similar results.

Conclusion

In conclusion, a small uniform interaction between e-neutrinos and matter is considered here. The coupled Dirac equations of the e, μ- neutrinos are solved for this interaction and the neutrino oscillations are computed. It is shown that the oscillation amplitude of the eneutrinos decreases in the presence of the interaction and their localization probability increases. Although the effect may be related to the solar neutrino problem, it is much weaker (V/ΔE ≪ 1) than what would be needed to explain the magnitude of the solar neutrino problem. It is likely that the solar neutrinos have a very small temperature, as a result of their extremely weak interaction with matter. Consequently, they may be viewed as being in their ground state, which is a Fermi sea. Since the electron and neutrino Compton wavelengths are close to each other we may expect an attractive neutrino-neutrino interaction from their forward scattering. This interaction may be mediated by the longitudinal compression solar density waves. Consequently, a superfluid ("superconducting") neutrino-pairing state may be expected. The combination of the weak interaction strength and the state density may lead to a critical temperature which lies above the neutrino temperature, and a corresponding energy gap. Therefore, a sizeable depletion of neutrino states might be expected to paired states. A paired state, extended in the whole space, can be viewed as a composite particle with internal cohesion energy; such a state would not be detectable, which may give a hint to the solar neutrino problem.

Acknowledgment

The author is indebted to his friends S. Stoica for bringing this problem to his attention and M. Horoi for useful comments. Also, the author is indebted to the members of the Laboratory of Theoretical Physics at Magurele-Bucharest for many fruitful discussions. This work has been supported by the Scientific Research Agency of the Romanian Government through Grants 04-ELI/2016 (Program 5/5.1/ ELI-RO), PN 16 4201 01/2016 and PN (ELI) 16 42 01 05/2016

Conflict of Interest

The author declares no conflict of interest.

References

1. Greiner W, Muller B (1996) Gauge theory of weak interactions. New York: Springer.

   [Google Scholar]

2. Kumaran S, Ludhova L, Penek O, Settanta G (2021) Borexino results on neutrinos from the Sun and Earth. Universe 7: 231.

   [Google Scholar]

3. Wolfenstein L (2018) Neutrino oscillations in matter. InSolar neutrinos. CRC Press.

   [Google Scholar]

4. Wolfenstein L (1979) Neutrino oscillations and stellar collapse. Phys Rev D. 20: 2634.

   [Google Scholar]

5. SP. Mikheyev, AYu. Smirnov (1985) Resonant amplification of neutrino oscillations in matter and spectroscopy of solar neutrinos. Sov J Nucl Phys 42: 913-917.
6. Mikheev SP, Smirnov AY (1986) Neutrino oscillations in a variable density medium and neutrino bursts due to the gravitational collapse of stars. Sov Phys JETP

   [Google Scholar]

7. Mikheyev SP, Smirnov AY (1989) Resonant neutrino oscillations in matter. Prog Par Nuc Phys 23: 41-136.

   [Google Scholar]

8. Bethe HA (2018) Possible explanation of the solar-neutrino puzzle. Phys Rev Lett 56: 1305-1308

   [Google Scholar] [PubMed]

9. Smirnov AY (2016) Solar neutrinos: Oscillations or No-oscillations?.

   [Google Scholar]

10. Mannheim PD (1988) Derivation of the formalism for neutrino matter oscillations from the neutrino relativistic field equations. Phys Rev D Part Fields 37: 1935.

    [Crossref] [Google Scholar] [PubMed]

11. Giunti C, Kim CW, Lee UW, Lam WP (1992) Majoron decay of neutrinos in matter. Phys Rev D Part Fields 45: 1557.

    [Crossref] [Google Scholar] [PubMed]

12. Giunti C, Kim CW, Lee UW (1992) Remarks on the weak states of neutrinos. Phys Rev D Part Fields 45: 2414.

    [Crossref] [Google Scholar] [PubMed]

13. Blasone M, Henning PA, Vitiello G (1999) The exact formula for neutrino oscillations. Phys Lett B 451: 140-145.

    [Google Scholar]

14. Horoi M (2020) On the MSW-like neutrino mixing effects in atomic weak interactions and double beta decays. Europ Physl J A. 56: 1-0.

    [Google Scholar]

15. Gonzalez-Garcia MC, Nir Y (2003) Neutrino masses and mixing: Evidence and implications. Rev Modern Phys. 75: 345.

    [Google Scholar]